
【题目】定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点。
已知数轴上A,B两点对应数分别为a和b,![]() ,P为数轴上一动点,对应数为x.
,P为数轴上一动点,对应数为x.
(1)a=______,b=_______;
(2)若点P为线段AB的中点,则P点对应的数![]() 为______________.若B为线段AP的中点时则P点对应的数
为______________.若B为线段AP的中点时则P点对应的数![]() 为______________。
为______________。
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动。
①设运动的时间为t秒,直接用含t的式子填空
AP=____________;BP=______________。
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?

【答案】(1)-2、4;(2)1、10;(3)①-3t+14或14-3t;20-3t或3t-20;②t=![]() ,t=
,t=![]() ,t=
,t=![]() .
.
【解析】
(1)根据非负数的性质解答即可;
(2)根据线段中点的定义得出规律:若A表示的数为a,B表示的数为b,P表示的数为x,P为线段AB的中点,则2x=a+b,然后根据这个规律解答即可.
(3)①根据题意得出A、B、P表示的数,从而得出结论;
②分三种情况讨论:若P为AB的中点,若A为BP的中点,若B为AP的中点,根据(2)得出的结论列方程求解即可.
(1)根据题意得:a+2=0,b-4=0,解得:a=-2,b=4.
故答案为:-2,4.
(2)∵P为线段AB的中点,∴AP=PB,∴x-a= b-x,∴2x=a+b,∴x=![]() =
=![]() =1;
=1;
若B为线段AP的中点,则2b=a+x,解得:x=2b-a=8-(-2)=10.
故答案为:1,10.
(3)由题意得:A表示的数为:-2-t,B表示的数为:4-t,P表示的数为:-16+2t.
①AP=|(-16+2t)-(-2-t)|=|14-3t|,BP=|(-16+2t)-(4-t)|=|20-3t|,∴AP=-3t+14或14-3t;BP=20-3t或3t-20.
故答案为:-3t+14或14-3t;20-3t或3t-20.
②分三种情况讨论:
若P为AB的中点,则:2(-16+2t)=(-2-t)+(4-t),解得:t=![]() ;
;
若A为BP的中点,则:2(-2-t)=(-16+2t)+(4-t),解得:t=![]() ;
;
若B为AP的中点,则:2(4-t)=(-2-t)+(-16+2t),解得:t=![]() .
.
综上所述:t的值为![]() 或
或![]() 或
或![]() 时,点A、点B、点P三点中其中一点是另外两点的中点.
时,点A、点B、点P三点中其中一点是另外两点的中点.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一方队正沿箭头所指的方向前进

(1)A的位置为第三列第四行,表示为(3,4),那么B的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)B左侧第二个人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)如果队伍向东前进,那么A北侧第二个人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(4)![]() 表示的位置是____________.
表示的位置是____________.
A.A B.B C.C D.D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90,AC=BC,AD平分∠CAB,DE⊥AB,垂足为E.
(1)求证:CD=BE;
(2)若AB=10,求BD的长度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
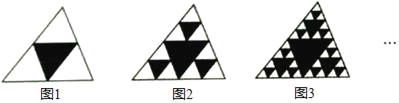
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限内及x轴,y轴上运动,第1分钟从原点运动到![]() ,第2分钟从
,第2分钟从![]() 运动到
运动到![]() ,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )
,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
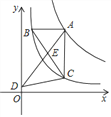
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com