
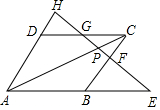
 如图,过?ABCD的对角线AC上任一点P作一直线,分别交AB、BC、CD、DA所在直线于E、F、G、H.求证:PE•PF=PG•PH.
如图,过?ABCD的对角线AC上任一点P作一直线,分别交AB、BC、CD、DA所在直线于E、F、G、H.求证:PE•PF=PG•PH. 分析 先利用平行四边形的性质得到CD∥AB,AD∥BC,则利用相似三角形的判定得到△PCG∽△PAE,△PCF∽△PAH,根据相似三角形的性质得$\frac{PC}{PA}$=$\frac{PG}{PF}$,$\frac{PC}{PA}$=$\frac{PF}{PH}$,利用等量代换得到$\frac{PG}{PF}$=$\frac{PF}{PH}$,然后根据比例的性质即可得到结论.
解答 解:∵四边形ABCD为平行四边形,
∴CD∥AB,AD∥BC,
∵CG∥AE,
∴△PCG∽△PAE,
∴$\frac{PC}{PA}$=$\frac{PG}{PF}$,
∵CF∥AH,
∴△PCF∽△PAH,
∴$\frac{PC}{PA}$=$\frac{PF}{PH}$,
∴$\frac{PG}{PF}$=$\frac{PF}{PH}$,
∴PE•PF=PG•PH.
点评 本题考查了相似三角形的判定于性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时主要根据相似比表示线段之间的关系.


科目:初中数学 来源: 题型:填空题
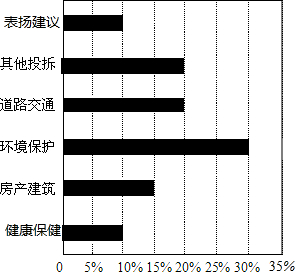 如图是一家报纸“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共30个.本周“百姓热线”共接到热线电话有100个.
如图是一家报纸“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共30个.本周“百姓热线”共接到热线电话有100个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{14}{3}$<a<-5 | B. | -5≤a<-$\frac{14}{3}$ | C. | -5<a≤-$\frac{14}{3}$ | D. | -$\frac{14}{3}$<a≤-5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com