
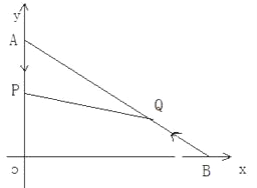
【题目】如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒.
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
【答案】(1)y=-![]() x+12;(2)
x+12;(2)![]() ,
,![]() ;(3)2,8;(4)5,20.
;(3)2,8;(4)5,20.
【解析】
试题(1)设直线AB的解析式为y=kx+b,解得k,b即可;
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t.②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
(3)根据△APQ的面积为![]() ,求出t的值.
,求出t的值.
(3)过点O作QE⊥AO于点E,利用t表示出△APQ的面积,利用函数的性质即可求解.
试题解析:(1)设直线AB的解析式为y=kx+b,
由题意,得![]()
解得: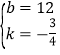
所以,直线AB的解析式为y=-![]() x+12;
x+12;
(2)由AO=12,BO=16得AB=20,
所以AP=t,AQ=20-2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以![]() ,
,
解得t=![]() (秒),
(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
所以![]() ,
,
解得t=![]() (秒);
(秒);
∴当t为![]() 秒或
秒或![]() 秒时,△APQ与△AOB相似;
秒时,△APQ与△AOB相似;
(3)过Q点作QE⊥Y轴于点E,
由△AQE∽△AOB知:![]()
即:![]()
解得:QE=![]()
又S△APQ=![]()
解得:![]() ,
,![]()
(4)∵QE=![]()
∴S△APQ=![]() APQE=
APQE=![]() t(
t(![]() )=-
)=-![]() t2+8t=-
t2+8t=-![]() (t-5)2+20
(t-5)2+20
∴当t=5时,△APQ的面积最大,最大面积是20个平方单位.
考点: 一次函数综合题.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合,且
重合,且![]() ),在射线
),在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
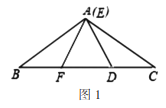
![]() 当点
当点![]() 在线段
在线段![]() 上时,
上时,
①若点![]() 与点
与点![]() 重合时,请说明线段
重合时,请说明线段![]() ;
;
②如图2,若点![]() 不与点
不与点![]() 重合,请说明
重合,请说明![]() ;
;
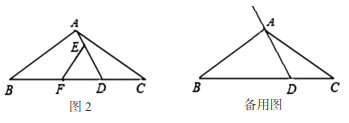
![]() 当点
当点![]() 在线段
在线段![]() 的延长线上
的延长线上![]() 时,用等式表示线段
时,用等式表示线段![]() 之间的数量关系(直接写出结果,不需要证明).
之间的数量关系(直接写出结果,不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读小强同学数学作业本上的截图内容并完成任务:
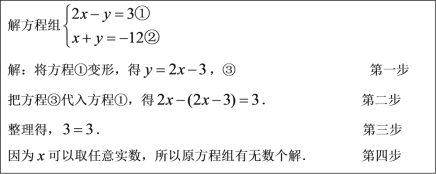
任务:
(1)这种解方程组的方法称为_____________;
(2)利用此方法解方程组的过程中所体现的数学思想是____________;(请你填写正确选项)
A.转化思想 B.函数思想 C.数形结合思想 D.公理化思想
(3)小强的解法正确吗?如果不正确,错在哪一步?请你求出正确的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+![]() θ,则∠BOC=( )
θ,则∠BOC=( )
A.90°﹣![]() θB.2θC.180°﹣θD.以上答案都不对
θB.2θC.180°﹣θD.以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC,AB=AC,点D在△ABC的外部,且∠DAC<90°,
(1)如图1,若AD=AC,求∠BDC;
(2)如图2,点E在线段AC上,线段DE的垂直平分线交BC的延长线于点P.当点D正好和点B关于线段AC的中点对称时,
①证明:△PDE为直角三角形;
②连接BE、AD,若![]() ,直接写出
,直接写出![]() =_____.
=_____.
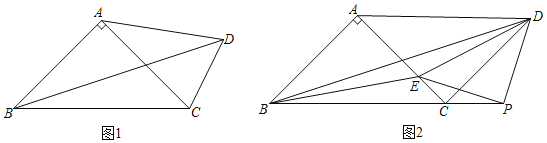
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
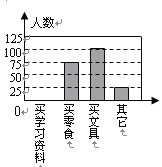
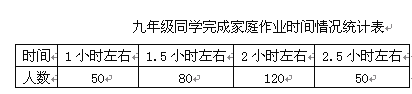
【题目】台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?

![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琳同学学习了《太阳光与影子》这一节以后,就想利用树影测量树高,但这棵树离大楼太近,影子不全落在地上,有一部分影子落在墙上(如图),她在某时刻测得留在墙上的影长为1.2 m,测得地面上的影长为2.7 m,巧的是她拿的竹竿的长也是1.2 m,竹竿的影长为1.08 m,她是怎样求得树高AB的?结果是多少?
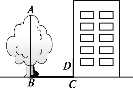
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:AC=AE;
(2)若△BDE的周长为20,求AB的长.
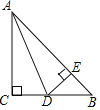
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com