
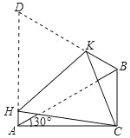
【题目】如图,在△ABC 中∠ACB=90°、∠CAB=30°,△ABD 是等边三角形将四边形 ACBD 折叠,使点 D 与点 C 重合,HK 为折痕,则cos∠ACH 的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
在Rt△ABC中,设BC=a,则AB=2BC=2a,AD=AB=2a.设AH=x,则HC=HD=AD-AH=2a -x.在Rt△ABC中,由勾股定理可求得得AC2=3a 2,在Rt△ACH中,由勾股定理得AH2+AC2=HC2,即x2+3a 2=(2a -x)2.解得x=![]() ,即AH=
,即AH=![]() .求得HC的值后,
.求得HC的值后,![]() 求值.
求值.
∵△ABD是等边三角形,
∴∠BAD=60°,AD=AB=BD
∵∠CAB=30°,
∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,设BC=a,
∴AB=2BC=2a.
∴AD=AB=2a.
设AH=x,则HC=HD=ADAH=2ax,
在Rt△ABC中,AC2=(2a)2a2=3a2,AC=![]()
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2ax) 2,
解得x=![]() ,即AH=
,即AH=![]() .
.
∴HC=2ax=2a![]() ,
,
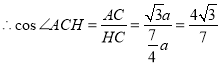 .
.
故选D.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】(感知)小亮遇到了这样一道题:已知如图在![]() 中,
中,![]() 在
在![]() 上,
上,![]() 在
在![]() 的延长上,
的延长上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
小亮仔细分析了题中的已知条件后,如图②过![]() 点作
点作![]() 交
交![]() 于
于![]() ,进而解决了该问题.(不需要证明)
,进而解决了该问题.(不需要证明)
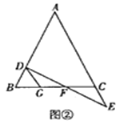
(探究)如图③,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
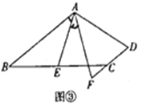
(应用)如图③,在正方形![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 边上的点,若
边上的点,若![]() =1,
=1,![]() =
=![]() ,∠
,∠![]() =90°,则
=90°,则![]() 的长为 .
的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2![]() ,求BD的长.
,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
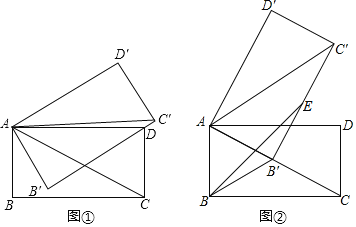
【题目】在矩形ABCD中,AB=2,∠ACB=30°,将矩形ABCD绕点A逆时针方向旋转,得到矩形AB′C′D′,记旋转角为α(0<α<90°).
(I)如图①,当B'C'过点D时,求△ADC'的面积S的值;
(Ⅱ)如图②,当点B的对应点B'落在AC上时,在B′C′上取点E,使B'E=AB.
①求∠EBB'的大小;
②求BE的长(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图①放置,其中![]() ,斜边
,斜边![]() ,把三角板
,把三角板![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,如图②,这时
,如图②,这时![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() .
.
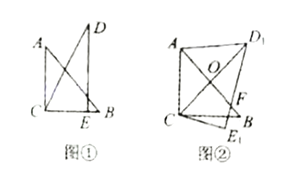
(1)求![]() 的度数;
的度数;
(2)求线段![]() 的长;
的长;
(3)若把![]() 绕着点
绕着点![]() 顺时针再旋转
顺时针再旋转![]() ,得
,得![]() .这时点
.这时点![]() 在
在![]() 的内部、外部,还是边上?请说明理由,
的内部、外部,还是边上?请说明理由,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习反比例函数的过程与方法,探究函数 y1=![]() (x≠0)的图象与性质,因为 y1=
(x≠0)的图象与性质,因为 y1=![]() =1﹣
=1﹣![]() ,即 y1=﹣
,即 y1=﹣![]() +1,所以我们对比函数 y=﹣
+1,所以我们对比函数 y=﹣![]() 来探究画出函数 y1=
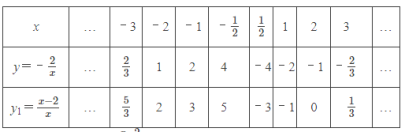
来探究画出函数 y1=![]() (x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
(x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
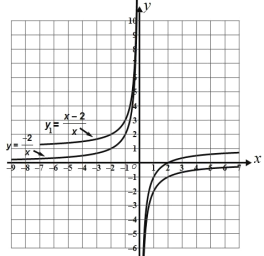
(1)观察:由 y1=![]() 图象可知:
图象可知:
①当 x>0 时,y 随 x的增大而 (填“增大”或“减小”)
②y1=![]() 的图象可以由 y=﹣
的图象可以由 y=﹣![]() 的图象向 平移 个单位长度得到.
的图象向 平移 个单位长度得到.
③y1 的取值范围是 .
(2)探究:①若直线 l 对应的函数关系式为 y2=kx+b,且经过点(﹣1,3)和点(1,﹣1),请再给出的平面直角坐标系中画出 y2,若 y1>y2,则 x 的取值范围为 .
②A(m1,n1),B(m2,n2)在函数 y=![]() 图象上,且 n1+n2=2,求 m1+m2 的值.
图象上,且 n1+n2=2,求 m1+m2 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
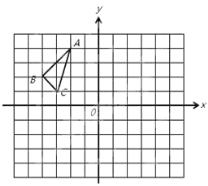
【题目】△ABC 在平面直角坐标系中的位置如图所示,其中每 个小正方形的边长为 1 个单位长度.
(1)画出△ABC 关于原点 O 的中心对称图形△A1B1C1,并写出点 A1 的坐标;
(2)将△ABC 绕点 C 顺时针旋转 90°得到△A2B2C,画出△A2B2C,求在旋转过程中,点 A 所经过的路径长
查看答案和解析>>
科目:初中数学 来源: 题型:
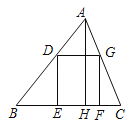
【题目】如图,四边形DEFG是△ABC的内接正方形,D、G分别在AB、AC上,E、F在BC上,AH是△ABC的高,已知BC=20,AH=16,求正方形DEFG的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.
(1)若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是 ;
(2)若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com