
【题目】某商场第1次用600元购进2B铅笔若干支,第2次用800元又购进该款铅笔,但这次每支的进价是第1次进价的八折,且购进数量比第1次多了100支.
(1)求第1次每支2B铅笔的进价;
(2)若要求这两次购进的2B铅笔按同一价格全部销售完毕后获利不低于600元,问每支2B铅笔的售价至少是多少元?
【答案】(1)第1次每支2B铅笔的进价为4元;(2)每支2B铅笔的售价至少是5元.
【解析】
(1)设第1次每支2B铅笔的进价为x元,则第2次的进价为0.8x元,根据数量=总价÷单价结合第二次比第一次多购进100支,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)根据数量=总价÷单价可求出第一次购进2B铅笔的数量,用其加100可求出第二次购进数量,设每支2B铅笔的售价为y元,根据利润=单价×数量﹣进价结合总利润不低于600元,即可得出关于y的一元一次不等式,解之取其最小值即可得出结论.
解:(1)设第1次每支2B铅笔的进价为x元,则第2次的进价为0.8x元,
依题意,得![]() ﹣
﹣![]() =100,
=100,
解得:x=4.
经检验,x=4是原方程的解,且适合题意.
答:第1次每支2B铅笔的进价为4元.
(2)600÷4=150(支),150+100=250(支)
设每支2B铅笔的售价为y元,
依题意,得:(150+250)y﹣(600+800)≥600,
解得:y≥5.
答:每支2B铅笔的售价至少是5元.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个在大矩形的面积,则n的最小值是 ( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠B=α,在AB、BC上分别找一点E、F,使△DEF的周长最小.此时,∠EDF=( )

A.αB.![]() C.
C.![]() D.180°-2α
D.180°-2α
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.

查看答案和解析>>
科目:初中数学 来源: 题型:
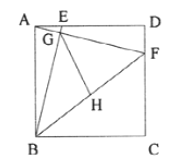
【题目】已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G. 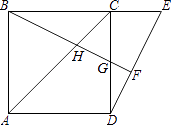
(1)求证:BG=DE;
(2)若点G为CD的中点,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com