
【题目】对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“生成三角形”.
(1)已知点A(4,0);
①若以线段OA为底的某等腰三角形恰好是点O,A的“生成三角形”,求该三角形的腰长;
②若Rt△ABC是点A,B的“生成三角形”,且点B在x轴上,点C在直线y=2x﹣5上,则点B的坐标为 ;
(2)⊙T的圆心为点T(2,0),半径为2,点M的坐标为(2,6),N为直线y=x+4上一点,若存在Rt△MND,是点M,N的“生成三角形”,且边ND与⊙T有公共点,直接写出点N的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②(1,0),(3,0)或(7,0);(2)点N的横坐标
;②(1,0),(3,0)或(7,0);(2)点N的横坐标![]() 的取值范围为
的取值范围为![]() .
.
【解析】
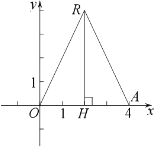
(1)①如图(见解析),设满足条件的三角形为等腰![]() ,过点R作
,过点R作![]() 于点H,由等腰三角形的性质得
于点H,由等腰三角形的性质得![]() ,再根据“生成三角形”的定义可得
,再根据“生成三角形”的定义可得![]() ,最后利用勾股定理即可得;
,最后利用勾股定理即可得;
②依题意,按点![]() 分别为直角顶点三种情况讨论,根据“生成三角形”的定义和直线
分别为直角顶点三种情况讨论,根据“生成三角形”的定义和直线![]() 的解析式分别建立等式,求解即可;
的解析式分别建立等式,求解即可;
(2)根据点![]() 分别为直角顶点三种情况讨论,根据“生成三角形”的定义、结合圆的切线性质列出等式,求解即可.
分别为直角顶点三种情况讨论,根据“生成三角形”的定义、结合圆的切线性质列出等式,求解即可.
(1)①如图,设满足条件的三角形为等腰![]() ,则
,则![]()
过点R作![]() 于点H
于点H
![]()
∵以线段OA为底的等腰![]() 恰好是点O,A的“生成三角形”
恰好是点O,A的“生成三角形”
![]()
在![]() 中,利用勾股定理得:
中,利用勾股定理得:![]()
故该三角形的腰长为![]() ;
;
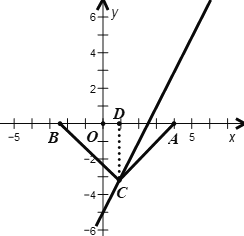
②依题意,分以下三种情况讨论:
当A为直角顶点时,则![]()
因点A的坐标为![]()
令![]() 代入
代入![]() 得
得![]() ,即
,即![]()
设点B的坐标为![]()
则![]() ,解得
,解得![]() 或
或![]()
故点B的坐标为![]() 或
或![]()
当B为直角顶点时,则![]()
设点B的坐标为![]() ,则
,则![]()
令![]() 代入
代入![]() 得
得![]() ,即
,即![]()
则有![]()
两边平方化简得![]() ,解得
,解得![]() 或
或![]()
故点B的坐标为![]() 或
或![]()
当C为直角顶点时,如图,过点C作![]() 于点D
于点D
设点D的坐标为![]() ,则
,则![]()
令![]() 代入
代入![]() 得
得![]()
由“生成三角形”的定义得![]()
则![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
令![]() ,则
,则![]()
化简得![]() ,此方程的根的判别式
,此方程的根的判别式![]() ,方程没有实数根
,方程没有实数根
则点C不能为![]() 的直角顶点
的直角顶点
综上,点B的坐标为![]() ,
,![]() 或
或![]() ;
;
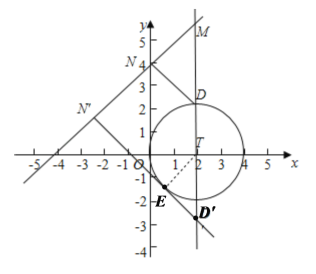
(2)当N为直角顶点时
由点M的坐标![]() 可知,点M在直线
可知,点M在直线![]() 上
上
由直线![]() 可知,
可知,![]()
则当点D在MT所在直线![]() 时,
时,![]() 是点M,N的“生成三角形”
是点M,N的“生成三角形”
如图,点N和![]() 是符合条件的两个临界位置
是符合条件的两个临界位置
由图可知,点D的坐标为![]() ,
,![]()
在![]() 中,
中,![]()
设点N的坐标为![]()
由两点之间距离公式得![]()
解得![]() ,再代入直线
,再代入直线![]() 得
得![]()
当点N在![]() 处时,图中
处时,图中![]() 也是符合条件的“生成三角形”
也是符合条件的“生成三角形”
此时,![]() 恰好与圆T相切,半径
恰好与圆T相切,半径![]()
则![]() 是等腰直角三角形,且
是等腰直角三角形,且![]()
![]()
则点![]() 的坐标为
的坐标为![]() ,设点
,设点![]() 的坐标为
的坐标为![]()
由两点之间距离公式得![]()
解得![]() ,再代入直线
,再代入直线![]() 得
得![]()
故当点N为直角顶点时,点N的横坐标![]() 的取值范围为
的取值范围为![]()
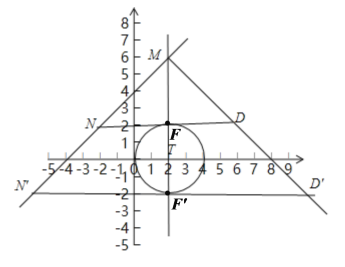
当点M为直角顶点时,![]()
如图,![]() 和
和![]() 均平行于x轴,且与圆T分别相切于点F,
均平行于x轴,且与圆T分别相切于点F,![]()
由平行线的性质和直线![]() 可知,
可知,![]()
则![]() 和
和![]() 都是等腰直角三角形
都是等腰直角三角形
因此,![]() 和
和![]() 都是符合条件的“生成三角形”, 此时,点N和
都是符合条件的“生成三角形”, 此时,点N和![]() 是符合条件的两个临界位置
是符合条件的两个临界位置
设点N的坐标为![]()
![]() 点F的坐标为
点F的坐标为![]()
![]() 点N的纵坐标为2,即
点N的纵坐标为2,即![]()
将![]() 代入
代入![]() 得
得![]()
同理可得![]()
故当点M为直角顶点时,点N的横坐标![]() 的取值范围为
的取值范围为![]()
当点D为直角顶点时,同(1)②中,当C为直角顶点时的思路一样,可证此时不存在符合条件的![]()
综上,点N的横坐标![]() 的取值范围为
的取值范围为![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】众志成城,抗击疫情,救助重灾区.某校某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):100,45,100,40,100,60,155.下面有四个推断:
①这7名同学所捐的零花钱的平均数是150;
②这7名同学所捐的零花钱的中位数是100;
③这7名同学所捐的零花钱的众数是100;
④由这7名同学所捐的零花钱的中位数是100,可以推断该校全体同学所捐的零花钱的中位数也一定是100.
所有合理推断的序号是( )
A.①③B.②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图2中阴影部分的周长与图1中阴影部分的周长的差为l,若要知道l的值,只要测量图中哪条线段的长( )
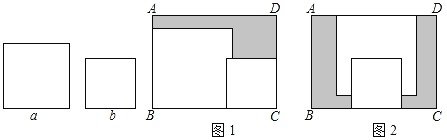
A.aB.bC.ADD.AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是我国建国70周年,回顾过去展望未来,创新是引领发展的第一动力,北京科技创新能力不断增强,下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况.
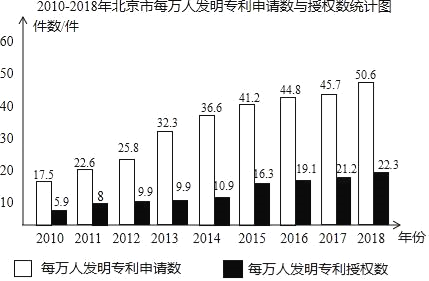
根据统计图提供的信息,下列推断合理的是( )
A. 2010﹣2018年,北京市毎万人发明专利授权数逐年增长
B. 2010﹣2018年,北京市毎万人发明专利授权数的平均数超过10件
C. 2010年申请后得到授权的比例最低
D. 2018年申请后得到授权的比例最高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y![]() 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若![]() ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC,作它的外接圆⊙O,连接AO并延长交⊙O于点D,交BC于点E,过点D作DF∥BC,交AC的延长线于点F.
(1)依题意补全图形并证明:DF与⊙O相切;
(2)若AB=6,求CF的长.
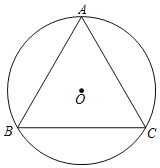
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出比重越低,居民家庭越富裕,反之越贫穷.
下面是根据从权威机构获得的部分数据绘制的统计图:
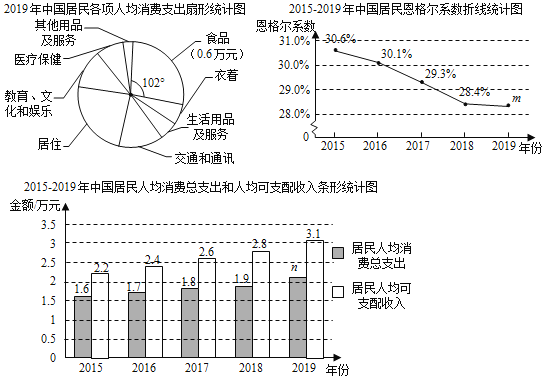
根据以上信息,回答下列问题:
(1)2019年中国城乡居民恩格尔系数m约为 (精确到0.1%);
(2)2019年居民人均消费总支出n约为 万元(精确到千位);
(3)下面的推断合理的是 .
①2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
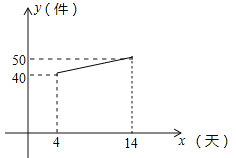
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com