
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
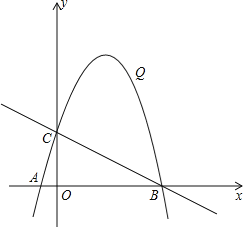
(1)求出△ABC的周长.
(2)在直线BC上方有一点Q,连接QC、QB,当△QBC面积最大时,一动点P从Q出发,沿适当路径到达y轴上的M点,再沿与对称轴垂直的方向到达对称轴上的N点,连接BN,求QM+MN+BN的最小值.
(3)在直线BC上找点G,K是平面内一点,在平面内是否存在点G,使以O、C、G、K为顶点的四边形是菱形?若存在,求出K的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,满足条件的点K的坐标为(
;(3)存在,满足条件的点K的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法求出A,B,C的坐标即可解决问题.
(2)如图1中,作QH∥OC交BC于H.设Q(m,![]() m2
m2![]() m+3
m+3![]() ),构建二次函数求出△BCQ的面积最大时Q的坐标,如图2中,作点Q关于y轴的对称点Q',在Q'Q上取一点Q″,使得Q'Q″=MN
),构建二次函数求出△BCQ的面积最大时Q的坐标,如图2中,作点Q关于y轴的对称点Q',在Q'Q上取一点Q″,使得Q'Q″=MN![]() ,连接Q″B交对称轴于N,作NM⊥y轴于M,连接QM,则此时QM+MN+BN的值最小.求出BQ″的长即可解决问题.
,连接Q″B交对称轴于N,作NM⊥y轴于M,连接QM,则此时QM+MN+BN的值最小.求出BQ″的长即可解决问题.
(3)分二种情形:当OC=CG时,可得菱形OCGK,菱形OCG'K'.当CG″是菱形的对角线时,可得菱形OCK″G″,分别求解即可解决问题.
(1)对于抛物线y![]() ,
,
令x=0,得到y=3![]() ,可得C(0,3
,可得C(0,3![]() ),
),
令y=0,得到x2﹣5x﹣6=0,解得:x=﹣1或6,
∴A(﹣1,0),B(6,0),
∴OA=1,OC=3![]() ,OB=6,
,OB=6,
∴AB=7,AC![]() 2
2![]() ,BC
,BC![]() 3
3![]() ,
,
∴△ABC的周长=7+2![]() 3
3![]() 7+5
7+5![]() .
.
(2)如图1中,作QH∥OC交BC于H.
设Q(m,![]() m2
m2![]() m+3
m+3![]() ),
),
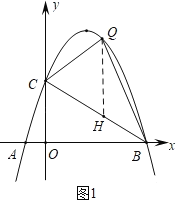
∵C(0,3![]() ),B(6,0),
),B(6,0),
∴直线BC的解析式为y![]() x+3
x+3![]() ,
,
∴H(m,![]() m+3
m+3![]() ),
),
∴QH![]() m2+3
m2+3![]() m,
m,
∴S△QBC![]() QH(Bx﹣x)
QH(Bx﹣x)![]() (
(![]() m2+3
m2+3![]() m)×6
m)×6
![]() (m﹣3)2
(m﹣3)2![]() ,
,
∵![]() 0,
0,
∴m=3时,△BCQ的面积最大,此时Q(3,6![]() ),
),
如图2中,作点Q关于y轴的对称点Q',在Q'Q上取一点Q″,
使得Q'Q″=MN![]() ,
,
连接Q″B交对称轴于N,作NM⊥y轴于M,连接QM,
则此时QM+MN+BN的值最小.
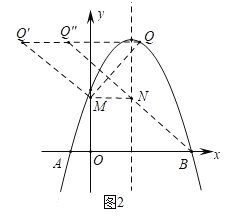
∵Q'(﹣3,6![]() ),Q'Q″
),Q'Q″![]() ,
,
∴Q″(![]() ,6
,6![]() ),
),
BQ″![]() ,
,
∵QM=MQ',四边形Q'Q″NM是平行四边形,
∴NQ″=MQ',
∴MQ+MN+BN=MN+NQ″++BN=MN+BQ″![]() ,
,
∴QM+MN+BN的最小值为![]() .
.
(3)如图3中,
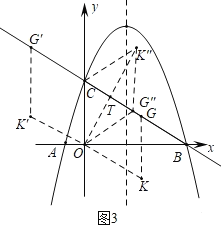
①当OC=CG时,可得菱形OCGK,菱形OCG'K'.
设G(m,![]() ).
).
∵GK∥CO,GK=CO,
∴K(m,![]() ).
).
∵OC=CG,
∴![]() ,
,
整理得:![]() ,
,
解得:m=![]() ,或m=
,或m=![]() .
.
当m=![]() 时,
时,![]() =
=![]() ,
,
此时G(![]() ,
,![]() ),K(
),K(![]() ,
,![]() );
);
当m=![]() 时,
时,![]() =
=![]() ,
,
此时G'(![]() ,
,![]() ),K'(
),K'(![]() ,
,![]() );
);
②当CG″是菱形的对角线时,可得菱形OCK″G″,设对角线的交点为T.
设G″(m,![]() ).
).
∵G″K″∥CO,G″K″=CO,
∴K″(m,![]() ).
).
∵OG″=CO,
∴![]() ,
,
整理得:![]() ,
,
解得:m=0(舍去),或m=![]() .
.
当m=![]() 时,
时,![]() =
=![]() ,此时G″(
,此时G″(![]() ,
,![]() ),K″(
),K″(![]() ,
,![]() ).
).
综上所述:满足条件的点K的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某校“综合实践”社团,计划利用![]() 长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为
长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为![]() .
.
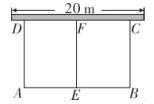
(1)能否围成总面积为![]() 的试验田?若能,求出
的试验田?若能,求出![]() 的长度;若不能,说明理由;
的长度;若不能,说明理由;
(2)能否围成总面积为![]() 的试验田?说说你的理由.
的试验田?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,且抛物线经过 A(1,0),C(0,3)两点,与x轴交于点B.
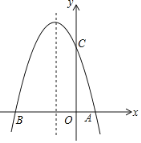
(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求此时点M的坐标;
(3)设点P为抛物线对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球和足球.已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握某次数学模拟考试卷的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
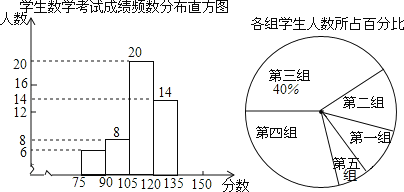
请将频数分布直方图补充完整;若老师找到第五组中一个学生的语文、数学、英语三科成绩,如表.老师将语文、数学、英语成绩按照3:5:2的比例给出这位同学的综合分数.求此同学的综合分数.
科目 | 语文 | 数学 | 英语 |
得分 | 120 | 146 | 140 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点.
(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求抛物线与x轴有两个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
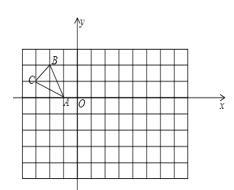
【题目】如图,在边长均为l的小正方形网格纸中,△ABC的顶点A、B、C均在格点上,O为直角坐标系的原点,点A(﹣1,0)在x轴上.
(1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧;
(2)分别写出B1、C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com