
【题目】在平面直角坐标系中,点A(4,0),B为第一象限内一点,且OB⊥AB,OB=2.
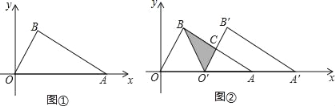
(1)如图①,求点B的坐标;
(2)如图②,将△OAB沿x轴向右平移得到△O′A′B′,设OO′=m,其中0<m<4,连接BO′,AB与O′B′交于点C.
①试用含m的式子表示△BCO′的面积S,并求出S的最大值;
②当△BCO′为等腰三角形时,求点C的坐标(直接写出结果即可).
【答案】(1)B(1,![]() );(2)①当m=2时,S最大=
);(2)①当m=2时,S最大=![]() ,②C(
,②C(![]() ,
,![]() ).
).
【解析】
(1)由OB⊥AB,0A=4,OB=2得出△AOB是有一个角为30°的直角三角形,简单计算即可;
(2)①由平移用m表示出BC,O′C,建立S=![]() [﹣(m﹣2)2+4],即可;
[﹣(m﹣2)2+4],即可;
②利用△BCO′为等腰三角形,则有CB=CO′确定出m,再利用相似求出CD,AD即可.
解:(1)∵OB⊥AB,0A=4,OB=2,
∴∠AOB=60°,∠OAB=30°,AB=2![]() ,
,
过点B作BE⊥OA,
∴OD=1,BE=![]() ,
,
∴B(1,![]() ).
).
(2)①∵△A′O′B′是△OAB平移得到,
∴∠A′O′B′=∠AOB=60°,O′B′⊥AB,
∵OO′=m,
∴AO′=4﹣m,
∴O′C=![]() AO′=
AO′=![]() (4﹣m),AC=
(4﹣m),AC=![]() AO′=
AO′=![]() (4﹣m),
(4﹣m),
∴BC=AB﹣AC=![]() m,
m,
∴S=![]() BC×O′C=
BC×O′C=![]() m(4﹣m)=
m(4﹣m)=![]() [﹣(m﹣2)2+4],
[﹣(m﹣2)2+4],
当m=2时,S最大=![]() .
.
②如下图,作BE⊥OA,CD⊥OA,

由①有,AO′=4﹣m,O′C=![]() (4﹣m),AC=
(4﹣m),AC=![]() (4﹣m),
(4﹣m),
∴CB=AB﹣AC=2![]() ﹣
﹣![]() (4﹣m)=
(4﹣m)=![]() m,
m,
由平移得,∠ACO′=∠ABO=90°,
∵△BCO′为等腰三角形,
∴CB=O′C,
∴![]() m=
m=![]() (4﹣m),
(4﹣m),
∴m=2(![]() ﹣1).
﹣1).
∵BE×OA=OB×AB,
∴BE=![]() =
=![]() ,
,
∴AE=![]() BE=3,
BE=3,
∵△ACO′∽△ABO,
∴![]() ,
,
∴CD=![]() ×BE=
×BE=![]() ×
×![]() =
=![]() =
=![]() ,
,
∵BE⊥OA,CD⊥OA,
∴BE∥CD,
∴![]() ,
,
∴AD=![]() ×AE=
×AE=![]() ,
,
∴OD=OA﹣AD=4﹣![]() =
=![]() ,
,
∴C(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
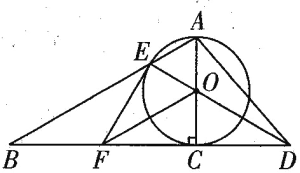
【题目】如图,以RtABC的直角边AC为直径作O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF//AB交BC于点F,连接EF、EC.
(1)求证:OFCE;
(2)求证:EF是O的切线;
(3)若O的半径为3,EAC60,求tanADE
查看答案和解析>>
科目:初中数学 来源: 题型:
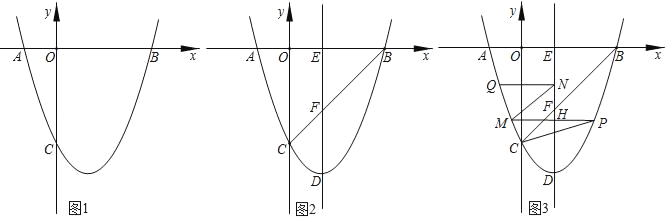
【题目】如图所示,平面直角坐标系中,O为坐标原点,二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 、B两点,与y轴交于点C;
、B两点,与y轴交于点C;
(1)求c与b的函数关系式;
(2)点D为抛物线顶点,作抛物线对称轴DE交x轴于点E,连接BC交DE于F,若AE=DF,求此二次函数解析式;
(3)在(2)的条件下,点P为第四象限抛物线上一点,过P作DE的垂线交抛物线于点M,交DE于H,点Q为第三象限抛物线上一点,作![]() 于N,连接MN,且
于N,连接MN,且![]() ,当
,当![]() 时,连接PC,求
时,连接PC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,
,![]() ,其对称轴在
,其对称轴在![]() 轴右侧,有下列结论:
轴右侧,有下列结论:
①抛物线经过点![]() ;
;
②方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
③![]() .
.
其中,正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
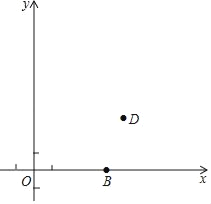
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,设它与
,设它与![]() 轴的另一个交点为
轴的另一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() 的面积是3.
的面积是3.
(1)求该抛物线的表达式;
(2)求![]() 的正切值;
的正切值;
(3)若抛物线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 在射线
在射线![]() 上,当
上,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年12月16﹣18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)

查看答案和解析>>
科目:初中数学 来源: 题型:
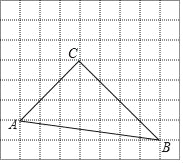
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.
(1)∠ACB的大小为 (度)
(2)在如图所示的网格中,以A为中心,取旋转角等于∠BAC,把△ABC逆时针旋转,请用无刻度的直尺,画出旋转后的△ABC,并简要说明旋转后点C和点B的对应点点C′和点B′的位置是如何而找到的(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
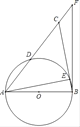
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com