
【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


【答案】(1)55m;(2)54.5m; (3)答案不唯一,如54.75 m或54.8 m
【解析】试题分析:(1)由题意,可得△ABC∽△DEC,根据相似三角形对应边的比等于相似比进行求解即可得;
(2)在Rt△ABC中,根据∠ACB的正切进行计算即可得;
(3)答案只要在上面两个小题的结果范围内即可.
试题解析:(1)由题意,可得△ABC∽△DEC,∴![]() ,
,
即![]() ,解得:AB=55,
,解得:AB=55,
答:该塔的高度为55m;
(2)在Rt△ABC中,tan∠ACB=![]() ,
,
∴AB=(48+2)×tan47.5°≈50×1.09=54.4(m),
答:该塔的高度为54.5m.
(3)答案不唯一,如54.75 m或54.8 m(数值在54.5~55之间均可).


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
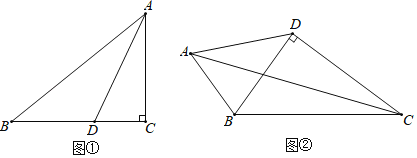
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
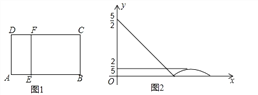
【题目】如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )
A. ![]() B. 5 C. 6 D.
B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两家服装商店销售同一品牌的西装和领带,西装定价都是每套200元,领带定价都是每条40元.现两家商店都在促销:甲店:买一套西装送一条领带;乙店:西装和领带都按定价的90%付款.
学校合唱团要购买西装20套,领带![]() 条(
条(![]() ),由后勤谢老师负责购买,请为谢老师出谋划策:
),由后勤谢老师负责购买,请为谢老师出谋划策:
(1)若只在一家商店购买,当![]() 时,谢老师选择哪家商店购买西装和领带更划算?
时,谢老师选择哪家商店购买西装和领带更划算?
(2)若只在一家商店购买,请用含![]() 的代数式分别表示在两家商店的花费;
的代数式分别表示在两家商店的花费;
(3)当![]() 时,请设计最省钱的购买方案并求出最少的花费是多少.
时,请设计最省钱的购买方案并求出最少的花费是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)写出该厂星期一生产工艺品的数量;
(2)本周产量最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,有理数![]() ,
,![]() ,
,![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() ,
,![]() ,
,![]() 三点,且
三点,且![]() ,
,![]() ,
,![]() 满足;①
满足;①![]() ;②多项式
;②多项式![]() 是关于
是关于![]() 的二次三项式.
的二次三项式.
(1)![]() ,
,![]() ,
,![]() 的值分别是 (直接写出答案);
的值分别是 (直接写出答案);
(2)若数轴上点![]() ,
,![]() 之间有一动点
之间有一动点![]() ,且点
,且点![]() 对应的数为
对应的数为![]() ,化简
,化简![]() ;
;
(3)若点![]() 在数轴上以每秒1个单位的速度向左运动,同时点
在数轴上以每秒1个单位的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和4个单位长度的速度向右运动(其中
个单位长度和4个单位长度的速度向右运动(其中![]() ),若在整个运动过程中,点
),若在整个运动过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求运动几秒后点
的距离差始终不变,求运动几秒后点![]() 与点
与点![]() 的距离为13个单位长度.
的距离为13个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于每个正整数![]() ,设
,设![]() 表示
表示![]() 的末位数字.例如:
的末位数字.例如:![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),…则
的末位数字),…则![]() 的值为( )
的值为( )
A.4040B.4038C.0D.4042
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com