
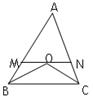
如图,OB、OC分别平分∠ABC与∠ACB, MN∥BC,若AB=36,AC=24,则△AMN的周长是
A、60 B、66 C、72 D、78
A
【解析】
试题分析:根据角平分线的性质可得∠ABO=∠OBC,再根据两直线平行,内错角相等可得∠OBC=BOM,从而得到∠ABO=∠BOM,根据等角对等边的性质可得BM=OM,同理可得CN=ON,然后求出△AMN的周长=AB+AC,最后代入数据进行计算即可得解.
∵OB平分∠ABC,
∴∠ABO=∠OBC,
∵MN∥BC,
∴∠OBC=BOM,
∴∠ABO=∠BOM,
∴BM=OM,
同理可得CN=ON,
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC,
∵AB=24,AC=36,
∴△AMN的周长=24+36=60,
故选A.
考点:平行线的性质,角平分线的性质
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
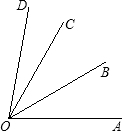 已知:如图,OB、OC分别为定角∠AOD内的两条动射线
已知:如图,OB、OC分别为定角∠AOD内的两条动射线查看答案和解析>>
科目:初中数学 来源: 题型:
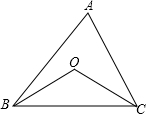
| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
 出结果)
出结果)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com