
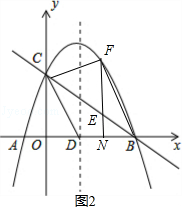
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
【答案】
(1)
解:把A(﹣1,0),C(0,2)代入y=﹣ ![]() x2+mx+n得
x2+mx+n得 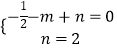 ,解得
,解得 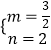 ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2;
x+2;
(2)
解:存在.
抛物线的对称轴为直线x=﹣ 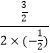 =
= ![]() ,
,
则D( ![]() ,0),
,0),
∴CD= ![]() =
= ![]() =
= ![]() ,
,
如图1,当CP=CD时,则P1( ![]() ,4);
,4);
当DP=DC时,则P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() ),
),
综上所述,满足条件的P点坐标为( ![]() ,4)或(
,4)或( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() );
);

(3)
解:当y=0时,=﹣ ![]() x2+
x2+ ![]() x+2=0,解得x1=﹣1,x2=4,则B(4,0),
x+2=0,解得x1=﹣1,x2=4,则B(4,0),
设直线BC的解析式为y=kx+b,
把B(4,0),C(0,2)代入得 ![]() ,解得
,解得 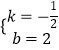 ,
,
∴直线BC的解析式为y=﹣ ![]() x+2,
x+2,
设E(x,﹣ ![]() x+2)(0≤x≤4),则F(x,﹣
x+2)(0≤x≤4),则F(x,﹣ ![]() x2+
x2+ ![]() x+2),
x+2),
∴FE=﹣ ![]() x2+
x2+ ![]() x+2﹣(﹣
x+2﹣(﹣ ![]() x+2)=﹣
x+2)=﹣ ![]() x2+2x,
x2+2x,
∵S△BCF=S△BEF+S△CEF= ![]() 4EF=2(﹣
4EF=2(﹣ ![]() x2+2x)=﹣x2+4x,
x2+2x)=﹣x2+4x,
而S△BCD= ![]() ×2×(4﹣
×2×(4﹣ ![]() )=
)= ![]() ,
,
∴S四边形CDBF=S△BCF+S△BCD
=﹣x2+4x+ ![]() (0≤x≤4),
(0≤x≤4),
=﹣(x﹣2)2+ ![]()
当x=2时,S四边形CDBF有最大值,最大值为 ![]() ,此时E点坐标为(2,1).
,此时E点坐标为(2,1).
【解析】(1)直接把A点和C点坐标代入y=﹣ ![]() x2+mx+n得m、n的方程组,然后解方程组求出m、n即可得到抛物线解析式;(2)先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣
x2+mx+n得m、n的方程组,然后解方程组求出m、n即可得到抛物线解析式;(2)先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣ ![]() ,则D(
,则D( ![]() ,0),则利用勾股定理计算出CD=
,0),则利用勾股定理计算出CD= ![]() ,然后分类讨论:如图1,当CP=CD时,利用等腰三角形的性质易得P1(
,然后分类讨论:如图1,当CP=CD时,利用等腰三角形的性质易得P1( ![]() ,4);当DP=DC时,易得P2(
,4);当DP=DC时,易得P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() );(3)先根据抛物线与x轴的交点问题求出B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣
);(3)先根据抛物线与x轴的交点问题求出B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣ ![]() x+2,利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征,设E(x,﹣
x+2,利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征,设E(x,﹣ ![]() x+2)(0≤x≤4),则F(x,﹣
x+2)(0≤x≤4),则F(x,﹣ ![]() x2+
x2+ ![]() x+2),则FE=﹣
x+2),则FE=﹣ ![]() x2+2x,由于△BEF和△CEF共底边,高的和为4,则S△BCF=S△BEF+S△CEF=
x2+2x,由于△BEF和△CEF共底边,高的和为4,则S△BCF=S△BEF+S△CEF= ![]() 4EF=﹣x2+4x,加上S△BCD=
4EF=﹣x2+4x,加上S△BCD= ![]() ,所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+
,所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+ ![]() (0≤x≤4),然后根据二次函数的性质求四边形CDBF的面积最大,并得到此时E点坐标.
(0≤x≤4),然后根据二次函数的性质求四边形CDBF的面积最大,并得到此时E点坐标.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF;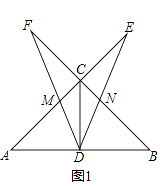
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( ) 
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产50件
D.若工人乙一天生产m(件),则他获得薪金4m元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深入贯彻党的十八大精神,我省某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A,B,C,D,E五个组,x表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
A组:90≤x≤100 B组:80≤x<90 C组:70≤x<80 D组:60≤x<70 E组:x<60
(1)参加调查测试的学生共有人;请将两幅统计图补充完整.
(2)本次调查测试成绩的中位数落在组内.
(3)本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的上边作正方形ADEF,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: . 
(2)数学思考:如图2,当点D在线段CB的延长线上时,以上①②关系是否成立,请在后面的横线上写出正确的结论.①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: . 
(3)如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出DG的长(写出求解过程).
BC,请求出DG的长(写出求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com