
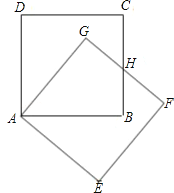
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
【答案】解:![]() .
.
证法1:连结![]() ,
,
![]() 四边形
四边形![]() ,
,![]() 都是正方形.
都是正方形.
![]()
![]() .
.
由题意知![]() ,又
,又![]() .
.
![]() ,
,
![]() .
.
证法2:连结![]() .
.
![]() 四边形
四边形![]() 都是正方形,
都是正方形,
![]() .
.
由题意知![]() .
.
![]() .
.
![]() .
.
![]() .
.
【解析】
试题要证明HG与HB是否相等,可以把线段放在两个三角形中证明这两个三角形全等,或放在一个三角形中证明这个三角形是等腰三角形,而图中没有这样的三角形,因此需要作辅助线,构造三角形.
试题解析:HG=HB,
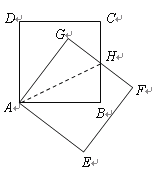
证法1:连接AH,
∵四边形ABCD,AEFG都是正方形,
∴∠B=∠G=90°,
由题意知AG=AB,又AH=AH,
∴Rt△AGH≌Rt△ABH(HL),
∴HG=HB.
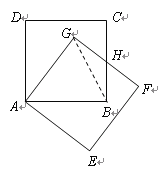
证法2:连接GB,
∵四边形ABCD,AEFG都是正方形,
∴∠ABC=∠AGF=90°,
由题意知AB=AG,
∴∠AGB=∠ABG,
∴∠HGB=∠HBG,
∴HG=HB.
考点;1.正方形的性质;2.全等三角形的判定.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相较于A,B两点(点A在点B的左侧),且点B的坐标为(1,0)
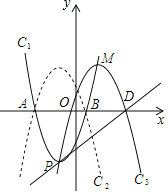
(1)求抛物线C1的函数解析式;
(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,抛物线C3的顶点为M,当点P,M关于点O成中心对称时.①求点M的坐标;②求抛物线C3的解析式;
(3)在(2)的条件下,设抛物线C3与x轴的正半轴交于点D,在直线PD的上方的抛物线C3上,是否存在点Q使得△PDQ的面积最大?若存在,求出当点Q的横坐标为何值时△PDQ面积最大,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车行销售甲、乙两种品牌的自行车,若购进甲品牌自行车5辆,乙品牌自行车6辆,需要进货款9500元,若购进甲品牌自行车3辆,乙品牌自行车2辆,需要进货款4500元.
(1)求甲、乙两种品牌自行车每辆进货价分别为多少元;
(2)今年夏天,车行决定购进甲、乙两种品牌自行车共50辆,在销售过程中,甲品牌自行车的利润率为![]() ,乙品牌自行车的利润率为
,乙品牌自行车的利润率为![]() ,若将所购进的自行车全部销售完毕后其利润不少于29500,那么此次最多购进多少辆乙种品牌自行车?
,若将所购进的自行车全部销售完毕后其利润不少于29500,那么此次最多购进多少辆乙种品牌自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费200元(含200元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分割线上时,则需重新转动转盘.
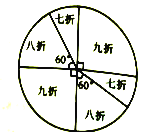
(1)某顾客正好消费220元,他转一次转盘,他获得九折、八折、七折优惠的概率分别是多少?
(2)某顾客消费中获得了转动一次转盘的机会,实际付费168元,请问他消费所购物品的原价应为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
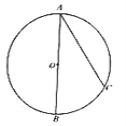
【题目】(本题9分)如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() .过点
.过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .请补全图形并解决下面的问题:
.请补全图形并解决下面的问题:
(1)求证:![]() ;
;
(2)如果![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
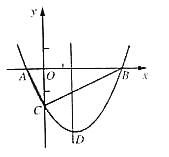
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是抛物线对称轴上的一个动点,当
是抛物线对称轴上的一个动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标及
的坐标及![]() 的最小周长.
的最小周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com