
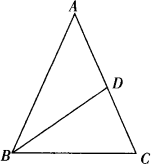
如图,已知在△ABC中,AB=AC,周长为16 cm,AC边上的中线BD把△ABC分成周长差为2 cm的两个三角形,求△ABC的各边长.
|
答案:∵AD=DC (1)当△ABD的周长-△BDC的周长=2 cm时,则(AB+BD+AD)-(BC+BD+CD)=AB-BC+(BD-BD)+(AD-CD)=AB-BC=2, 又∵AB+BC+AC=16,且AB=AC,故2AB+BC=16,∴AB=6,BC=4. 此时,△ABC的各边长为AB=AC=6 cm,BC=4 cm. (2)当△BDC的周长-△ABD的周长=2 cm时,有BC-AB=2,又2AB+BC=16, ∴AB= |
|
本题渗透着分类思想,应考虑腰长大于底边或腰长小于底边两种情况(即周长之差为2),同时还要注意求得的三角形三边长是否符合题意,这是我们在后面要学到的,本题的两种结果都符合要求,这一点将在后面讨论. |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com