Question

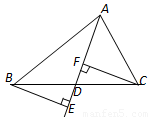
如图，已知BE⊥AD，CF⊥AD，且BE＝CF．

（1）请你判断AD是△ABC的中线还是角平分线？并证明你的结论．

（2）在（1）的条件下，若AB＝6，AC＝4，请确定AD的值范围．

 

 

 

Answer 1

【答案】

解：（1）AD是△ABC的中线.

理由如下：∵BE⊥AD，CF⊥AD，∴∠BED＝∠CFD＝90°

又∵BE＝CF，∠BDE＝∠CFD　∴△BDE≌△CFD（AAS）

∴BD＝CD ，即AD是△ABC的中线.

（2）过点B作BG∥AC交AD延长线于点G，

∴∠GBD＝∠ACD，.

又∵AD是中线，∠BDG＝∠ADC，

∴△BDG≌△CDA（ASA），

∴BG＝AC＝4，AD＝GD，

在△ABG中，AB＝6，根据三角形三边关系，

∴2＜AG＜10，

∴1＜AD＜5.

【解析】（1）证得三角形全等可得对应边BD＝CD，即可知AD是△ABC的中线；

       （2）三角形任意两边之和大于第三边，两边之差小于第三边。