解:(1)∵a≠0,abc=0,
∴bc=0
当b=0时:
由

,
得
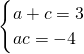
,
解得
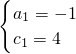
.
或
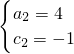
∵a<b<c.
∴
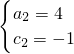
(不合题意,舍去)
∴a=-1,b=0,c=4
<2>当c=0时
由

,
得
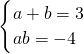
解之得
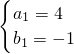
.
或
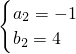
,
∵a<b<c;
∴
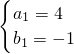
和
,都不合题意,舍去.
∴所求的抛物线解析式为y=-x
2+4.
(2)①在y=-x
2+4中,当y=0时,x=±2;当x=0时,y=4.
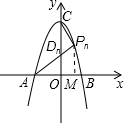
∴A、B、C三点的坐标分别为(-2,0),(2,0),(0,4)
过P作PG⊥x轴于G,
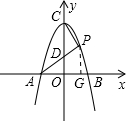
设点P坐标为(m,n)
∵点P是这条抛物线上第一象限内的点
∴m>0,n>0,n=-m
2+4
∴PG=-m
2+4,OA=2,AG=m+2
∵OD∥PG,OD=1.5
∴
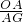
=
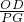
即
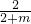
=
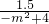
解得m
1=

,m
2=-2(不合题意,舍去)
∴OG=

又CD=OC-OD=4-1.5=2.5
S
△PDC=

•CD•OG=

×

×

=

S
△AOD=

•OA•OD=

×

×2=

=
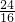
∴S
△PDC>S
△AOD又∵S
△APC=S
△PDC+S
△ADC,S
△AOC=S
△AOD+S
△ADC
∴S
△APC>S
△AOC②分两种情况讨论:
在第一象限内,设在抛物线上存在点Pn(m,n),使得S
△APnC=S
△AOC.
过Pn作PnM⊥x轴于点M,
则m>0,n>0,n=-m
2+4
OM=m,PnM=-m
2+4,OA=2,AM=m+2
设APn交y轴于点Dn,设ODn=t
∵ODn∥PnM,
∴
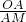
=
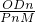
即
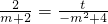
化简为mt+2t=8-2m
2,DnC=OC-ODn=4-t
S
△AODn=

OA•ODn=

×2×t=t;
S
△PnCDn=

CDn•OM=

(4-t)×m;
∵S
△AOC=S
△APnC
∴S
△AODn=S
△PnCDn即t=

(4-t)×m,mt+2t=4m
将mt+2t=4m代入mt+2t=8-2m
2中有8-2m
2=4m
整理得m
2+2m-4=0,m
1=

-1,m
2=-1-

∵m>0,
∴m
2=-1-

(不合题意,舍去)
∴m=

-1,
此时n=-m
2+4=-(

-1)
2+4=2

-2
∴存在点Pn坐标为(

-1,2

-2),
使得S
△APnC=S
△AOC在第二象限内,这条抛物线上任取一点Pnn,连接PnnA,PnnC,分别过点A作直线l
1垂直x轴,过点C作直线l
2垂直于y轴,l
1与l
2相交于Q点,则四边形QAOC是矩形,S
△AQC=S
△AOC.
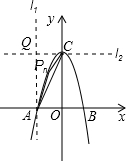
设Pnn点坐标为(mn,nn)
则有-2<mn<0
∵nn=-m
n2+4
∴0<nn<4
∴点Pn
n在矩形QAOC内,又易知Pnn在△AQC内
∴S
△APnC<S
△AQC,S
△APnC<S
△AOC
∴在第二象限内这条抛物线上不存在点Pnn,使S
△APnC=S
△AOC.
分析:(1)已知了四个条件:abc=0 ①;a+b+c=3②;ab+bc+ca=-3③;a<b<c④.
根据①可知b=0或c=0(a≠0),那么本题可分两种情况进行讨论:
一:当b=0,可联立②③,求出a,c的值,然后根据④判断出符合条件的a,c的值,进而可求出抛物线的解析式.
二:当c=0时,方法同一.
综合两种情况可得出抛物线的解析式.
(2)①比较S
△APC和S
△AOC的大小实际就是比较△DPC和△AOD的面积.
△AOD中,根据OA,OD的长,可求出△AOD的面积.
△DPC中,可以CD为底边,P点的纵坐标为高,
过P作PG⊥x轴于G,OG就是△DPC的高.
可根据相似三角形ADO和APG,得出关于OD,PG,OA,OG的比例关系式.
设出P点的坐标,即可根据所得的比例关系式求出P点的坐标,从而可求出△DPC的面积.
然后比较△DPC和△AOD的面积即可得出S
△APC和S
△AOC的大小.
②本题要分两种情况进行讨论:
当P点在第一象限时,解法同①,只不过要设出P点的坐标和OD的长,其他解法基本一样,只是最后不是比较大小,而是得出一个等量关系.根据这个等量关系来求P点的坐标.
可分别过C,A作坐标轴的平行线,可得出一个矩形,设两条平行线的交点为Q,那么△AQC与△AOC的面积相等,而P在△ACQ内,因此△ACP的面积总小于△ACQ的面积.因此△ACP的面积不会和△ACO的面积相等.此种情况不成立.
点评:本题结合三角形的相关知识考查了二次函数的综合应用,由于题中的数据较多,计算过程较复杂,因此细心求解是解题的关键.

 ,
,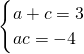 ,
,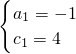 .
.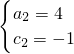
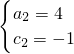 (不合题意,舍去)
(不合题意,舍去) ,
,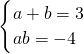
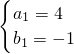 .
.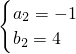 ,
,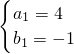 和
和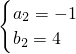 ,都不合题意,舍去.
,都不合题意,舍去.
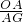 =
=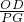
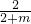 =
=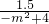
 ,m2=-2(不合题意,舍去)
,m2=-2(不合题意,舍去)
 •CD•OG=
•CD•OG= ×
× ×
× =
=
 •OA•OD=
•OA•OD= ×
× ×2=
×2= =
=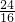

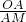 =
=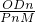
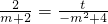
 OA•ODn=
OA•ODn= ×2×t=t;
×2×t=t; CDn•OM=
CDn•OM= (4-t)×m;
(4-t)×m; (4-t)×m,mt+2t=4m
(4-t)×m,mt+2t=4m -1,m2=-1-
-1,m2=-1-
 (不合题意,舍去)
(不合题意,舍去) -1,
-1, -1)2+4=2
-1)2+4=2 -2
-2 -1,2
-1,2 -2),
-2),


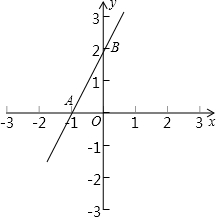
 一条抛物线y=
一条抛物线y=
 已知抛物线y=ax2+bx+c经过A(1,-4),B(-1、0),C(-2,5)三点.
已知抛物线y=ax2+bx+c经过A(1,-4),B(-1、0),C(-2,5)三点.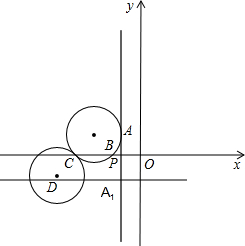 A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P
A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P