
【题目】在平面直角坐标系xOy中,抛物线y=mx2+6mx+n(m>0)与x轴交于A,B两点(点A在点B左侧),顶点为C,抛物线与y轴交于点D,直线BC交y轴于E,S△ABC:S△AEC = 2∶3.
(1)求点A的坐标;
(2)将△ACO绕点C顺时针旋转一定角度后,点A与B重合,此时点O恰好也在y轴上,求抛物线的解析式.
【答案】(1)A(-5,0);(2)![]() .
.
【解析】试题分析:由x=![]() 的抛物线的对称轴,分两种情况对S△ABC:S△AEC进行讨论;
的抛物线的对称轴,分两种情况对S△ABC:S△AEC进行讨论;
(2)由(1)知符合要求的点A有两种情况,分别代入即可求得抛物线的解析式.
试题解析:(1)抛物线y=mx2+6mx+n(m>0),得到对称轴x=-3,
①当S△ABC:S△AEC=2∶3时,BC:CE=2:3,
∴CB:BE=2:1
∵OF=3,∴OB=1,即B(-1,0)
∴A(-5,0),B(-1,0),
②当S△ABC:S△AEC=3∶2时,BC:CE=3:2,
∴CD:BD=2:1
∴A(-![]() ,0),B(
,0),B(![]() ,0);
,0);
(2)①当A(-5,0),B(-1,0)时,
把B(-1,0)代人y=mx2+6mx+n得,n=5m,
m=![]() ,n=
,n=![]() ,
,
∴y=![]() x+
x+![]() x+
x+![]() ;
;
②当A(-![]() ,0),B(
,0),B(![]() ,0)时,
,0)时,
把B(![]() ,0)代人y=mx2+6mx+n得,n=
,0)代人y=mx2+6mx+n得,n=![]() m,
m,
m=![]() ,n=
,n= ![]() ,
,
∴y=![]() x+
x+![]() x
x![]() .
.


科目:初中数学 来源: 题型:
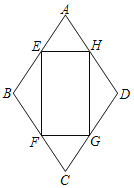
【题目】如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.
(1)求S关于x的函数解析式;
(2)当EFGH是正方形时,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书.甲图书每本价格是乙图书每本价格的2.5倍,如果用900元购买图书,则单独购买甲图书比单独购买乙图书要少18本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总费用不超过1725元,那么该图书馆最多可以购买多少本乙图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,商洛剧院举行专场音乐会,成人票每张20元,学生票每张5元,为了吸引广大师生来听音乐会,剧院制定了两种优惠方案:
方案一:购买一张成人票赠送一张学生票;
方案二:成人票和学生票都打九折.
我校现有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为![]() (人),付款总金额为
(人),付款总金额为![]() (元),请分别确定两种优惠方案中
(元),请分别确定两种优惠方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)请你结合参加听音乐会的学生人数,计算说明怎样购票花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
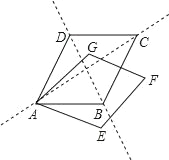
【题目】如图,菱形ABCD和菱形AEFG开始完全重合,现将菱形AEFG绕点A顺时针旋转,设旋转角∠BAE=α(0°<α<360°),则当α=_____时,菱形的顶点F会落在菱形ABCD的对角线所在的直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com