
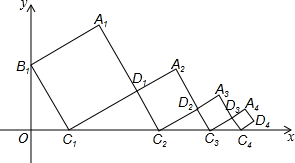
 如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )| A. | ($\frac{\sqrt{3}}{3}$)2014×($\frac{1+\sqrt{3}}{2}$) | B. | ($\frac{\sqrt{3}}{3}$)2015($\frac{1+\sqrt{3}}{2}$) | C. | ($\frac{\sqrt{3}}{2}$)2014×($\frac{1+\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{2}$)2015×($\frac{1+\sqrt{3}}{3}$) |
分析 首先根据正方形的性质和锐角三角函数求得第1个,第2个,第3个正方形的边长,归纳第2015和第2016个小正方形的边长,根据A1,A2,A3…的纵坐标可得A2015的纵坐标.
解答 解:设A1,A2,A3…A2015的纵坐标分别为y1,y2,y3…y2015,
∵D1 C2=$\frac{1}{tan60°}$=$\frac{\sqrt{3}}{3}$,D2C3=$\frac{\frac{\sqrt{3}}{3}}{\sqrt{3}}$=$\frac{1}{3}$=($\frac{\sqrt{3}}{3}$)2,D3C4=$(\frac{\sqrt{3}}{3})^{3}$,…,
∴D2015C2016=$(\frac{\sqrt{3}}{3})^{2015}$,
∵y1=(A1D1+D1C2)•sin60°=(1$+\frac{\sqrt{3}}{3}$)$\frac{\sqrt{3}}{2}$,
y2=[$\frac{\sqrt{3}}{3}$$+(\frac{\sqrt{3}}{3})^{2}$]$•\frac{\sqrt{3}}{2}$,…,
∴y2015=[($\frac{\sqrt{3}}{3}$)2014+($\frac{\sqrt{3}}{3}$)2015]•$\frac{\sqrt{3}}{2}$=$(\frac{\sqrt{3}}{3})^{2014}$(1+$\frac{\sqrt{3}}{3}$)•$\frac{\sqrt{3}}{2}$=$(\frac{\sqrt{3}}{3})^{2014}$×($\frac{\sqrt{3}+1}{2}$),
故选A.
点评 本题主要考查了正方形的性质和规律的归纳探究,利用正方形的性质发现每个小正方形的边长是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )| A. | $\frac{1}{2}$π-1 | B. | $\frac{1}{2}$π-2 | C. | π-2 | D. | π-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
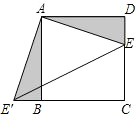 如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $2\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
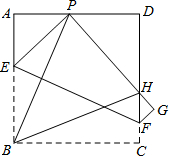 如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题
如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015“两相和”杯群星演唱会在我市体育馆进行,市文化局、广电局
2015“两相和”杯群星演唱会在我市体育馆进行,市文化局、广电局查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
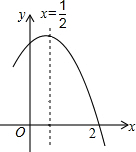 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com