
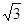 ,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
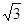 ≈1.73,精确到0.1米)。(5分)
≈1.73,精确到0.1米)。(5分)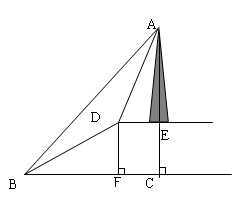
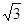 ,所以tanDBF=
,所以tanDBF=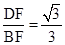 ,所以
,所以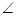 DBF=30°。所以Rt△DBF中,DF=
DBF=30°。所以Rt△DBF中,DF=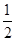 BD=25m,易知DE与BC为水平线,所以四边形DEFC为长方形,CE=DF=25m。
BD=25m,易知DE与BC为水平线,所以四边形DEFC为长方形,CE=DF=25m。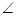 BDA=360°-
BDA=360°-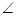 BDF-
BDF-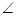 FDE-
FDE-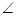 ADE=150°。又∵
ADE=150°。又∵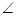 ABC=45°,
ABC=45°,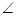 DBF=30°∴
DBF=30°∴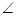 ABD=15°,∴
ABD=15°,∴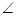 BAD=180°-
BAD=180°-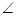 ABD-
ABD-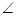 BDA=15°∴
BDA=15°∴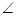 BAD=
BAD=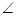 ABD,△ADB为等腰三角形,所以AD=BD=50m。在Rt△ADE中,∵
ABD,△ADB为等腰三角形,所以AD=BD=50m。在Rt△ADE中,∵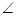 ADE=60°,∴AE=
ADE=60°,∴AE= =
= ≈43.3m
≈43.3m

科目:初中数学 来源:不详 题型:解答题
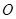 ,铁环钩与铁环相切点为
,铁环钩与铁环相切点为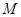 ,铁环与地面接触点为
,铁环与地面接触点为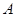 ,
,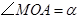 ,且
,且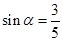 .
.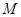 离地面
离地面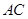 的高度
的高度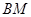 (单位:厘米);
(单位:厘米);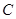 与点
与点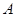 的水平距离
的水平距离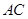 等于
等于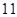 个单位,求铁环钩MP的长度(厘米).
个单位,求铁环钩MP的长度(厘米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com