
【题目】如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;
(1)求抛物线的解析式;
(2)点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;
(3)在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.
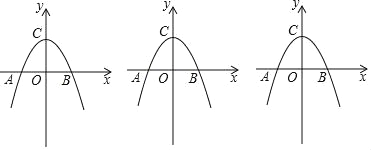
【答案】(1)y=﹣![]() x2+2;(2)S=﹣
x2+2;(2)S=﹣![]() t2+t(0<t<2);S═
t2+t(0<t<2);S═![]() t2﹣t(2<t≤4);(3)
t2﹣t(2<t≤4);(3)![]() .
.
【解析】
(1)把A点坐标代入二次函数,解得a=-![]() ,即可求解;
,即可求解;
(2)利用S=![]() CQOP,分0<t<2、2<t≤4两种情况求解即可;
CQOP,分0<t<2、2<t≤4两种情况求解即可;
(3)过点G作GH⊥y轴,利用HG∥OP,得![]() =
=![]() ,求出GH=
,求出GH=![]() ,利用GE=EC+CG=即可求解.
,利用GE=EC+CG=即可求解.
解:(1)把A点坐标代入二次函数,解得a=﹣![]() ,
,
故:二次函数的表达式为:y=﹣![]() x2+2;
x2+2;
(2)S=![]() CQOP,
CQOP,
当0<t<2时,
S=![]() t(﹣t+2)=﹣
t(﹣t+2)=﹣![]() t2+t,
t2+t,
当2<t≤4时,
S═![]() t(t﹣2)=
t(t﹣2)=![]() t2﹣t;
t2﹣t;
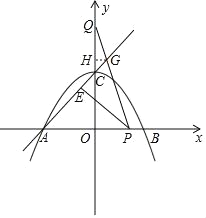
(3)t秒时,AP=t,OP=t﹣2,CQ=t,
直线AC与x轴的夹角为45°,
则AE=![]() ,GC=
,GC=![]() GH,AC=2
GH,AC=2![]() ,HC=HG,
,HC=HG,
过点G作GH⊥y轴,交y轴于点H,
∵HG∥OP,
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
解得:GH=![]() ,
,
则:GC=![]() GH=
GH=![]()
GE=EC+CG=AC﹣AE+GC=2![]() ﹣
﹣![]() +
+![]()
![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
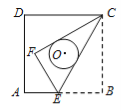
【题目】如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
A.4![]() B.
B. ![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译![]() 若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
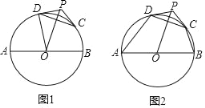
【题目】如图1,AB是⊙O的直径,P为⊙O外一点,C,D为⊙O上两点,连结OP,CD,PD=PC.已知AB=8.
(1)若OP=5,PD=3,求证:PD是⊙O的切线;
(2)若PD、PC是⊙O的切线;
①求证:OP⊥CD;
②连结AD,BC,如图2,若∠DAB=50°,∠CBA=70°,求弧CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
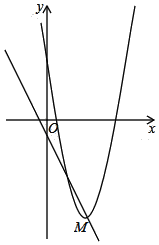
【题目】在平面直角坐标系中,抛物线![]() 的顶点M在直线L:
的顶点M在直线L:![]() 上.
上.
![]() 求直线L的函数表达式;
求直线L的函数表达式;
![]() 现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当
现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当![]() 时,求平移后的抛物线的解析式.
时,求平移后的抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com