
如图,抛物线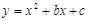 与
与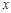 轴交于A(-1,0),B(3,0) 两点.
轴交于A(-1,0),B(3,0) 两点.
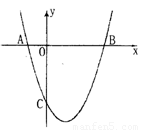
(1) 求该抛物线的解析式;
(2) 设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3) 设(1)中抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(1) y=x2-2x-3(2) 当P点的坐标分别为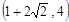 、
、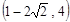 、(1,-4)时,S△PAB=8. (3) 点Q的坐标为(1,-2)
、(1,-4)时,S△PAB=8. (3) 点Q的坐标为(1,-2)
【解析】(1)∵抛物线y=x2+bx+c与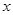 轴的两个交点分别为A(-1,0),B(3,0)
轴的两个交点分别为A(-1,0),B(3,0)
∴ 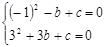 ┄ 2分
┄ 2分
解之,得 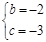 ┄ 3分
┄ 3分
∴所求抛物线的解析式为:y=x2-2x-3 ┄ 4分
(2)设点P的坐标为(x,y),由题意,得
S△ABC=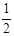 ×4×|y|=8
┄ 5分
×4×|y|=8
┄ 5分
∴|y|=4, ∴ y=±4 ┄ 6分
当y=4时, x2-2x-3=4
∴ x1=1+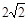 ,
x2=1-
,
x2=1-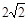 ┄ 7分
┄ 7分
当y=-4时,x2-2x-3=-4 ∴ x=1 ┄ 8分
∴当P点的坐标分别为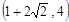 、
、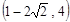 、(1,-4)时,S△PAB=8. ┄ 9分
、(1,-4)时,S△PAB=8. ┄ 9分
(3) 解法1: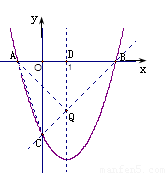
在抛物线y=x2-2x-3的对称轴上存在点Q, 使得ΔQAC的周长最小. ┄ 10分
∵AC长为定值,∴要使ΔQAC的周长最小,只需QA+QC最小.
∵点A关于对称轴x=1的对称点是B(3,0),
抛物线y=x2-2x-3与y轴交点C的坐标为(0,-3)
∴由几何知识可知,Q是直线BC与对称轴x=1的交点 ┄ 11分
设直线BC的解析式为y=kx-3.
∵直线BC过点B(3,0) ∴ 3k-3=0 ∴ k=1.
∴直线BC的解析式为 y=x-3 ┄ 12分
∴当x=1时,y=-2.
∴点Q的坐标为(1,-2). ┄ 13分
(3) 解法2:
在抛物线y=x2-2x-3的对称轴上存在点Q ,使得ΔQAC的周长最小. ┄ 10分
∵AC长为定值,∴要使ΔQAC的周长最小,只需QA+QC最小
∵点A关于对称轴x=1的对称点是B(3,0),
抛物线y=x2-2x-3与y轴交点C的坐标为(0,-3)
∴由几何知识可知,Q是直线BC与对称轴x=1的交点. ┄ 11分
∵OC∥DQ,
∴ΔBDQ∽ΔBOC.
∴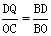 ,即
,即 .
┄ 12分
.
┄ 12分
∴DQ=2. ∴点Q的坐标为(1,-2). ┄ 13分
(1)已知了抛物线过B、C两点,而抛物线的解析式中也只有两个待定系数,因此可将B、C的坐标代入抛物线的解析式中,即可求出待定系数的值,也就得出了二次函数的解析式.
(2)根据(1)中得出的抛物线的解析式,可求得A点的坐标,也就能得出AB的长.△PAB中,AB的长为定值,那么可根据△PAB的面积求出P到AB的距离,即P点纵坐标的绝对值,然后将其代入抛物线的解析式中(分正负两个值)即可求出P点的坐标.
(3)本题的关键是找出Q点的位置,已知了B与A点关于抛物线的对称轴对称,因此只需连接BC,直线BC与对称轴的交点即为Q点.可根据B、C两点的坐标先求出直线BC的解析式,然后联立抛物线对称轴的解析式即可求出Q点的坐标.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
如图,抛物线与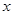 轴交于
轴交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 是方程
是方程![]() 的两个根。(14分)
的两个根。(14分)
(1)求抛物线的解析式;
 (2)点
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)点![]() 在(1)中抛物线上,
在(1)中抛物线上,
点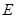 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是
轴上是
否存在点 ,使以
,使以![]() 为顶
为顶
点的四边形是平行四边形,如果存在,
求出所有满足条件的点![]() 的坐标,
的坐标,
若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线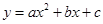 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、![]() ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值![]() 相等.
相等.
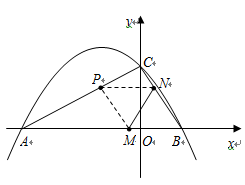
1.求a、b、c的值;
2.若点![]() 同时从
同时从![]() 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿![]() 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结![]() ,将
,将![]() 沿
沿![]() 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时,![]() 点恰好落在
点恰好落在![]() 边上的
边上的![]() 处?并求点
处?并求点![]() 的坐标及四边形
的坐标及四边形![]() 的面积;
的面积;
3.上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
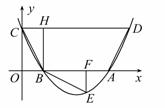
如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于C点,四边形OBHC为矩形,CH的延长
轴交于C点,四边形OBHC为矩形,CH的延长![]() 线交抛物线于点D(5,2),连结BC、AD.
线交抛物线于点D(5,2),连结BC、AD.
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90º后再沿![]() 轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013届四川省盐边县红格中学九年级下学期摸底考试数学试卷(带解析) 题型:解答题
如图,抛物线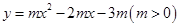 与
与 轴交于
轴交于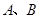 两点,与
两点,与 轴交于
轴交于 点.
点.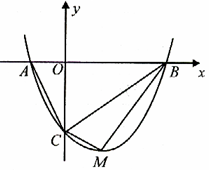
(1)请求出抛物线顶点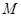 的坐标(用含
的坐标(用含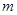 的代数式表示),
的代数式表示),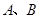 两点的坐标;
两点的坐标;
(2)经探究可知, 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;
(3)是否存在使 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届仙师中学九年级第一次月考试考试数学卷 题型:选择题
如图,抛物线与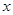 轴交于
轴交于 (
( ,0)、
,0)、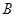 (
( ,0)两点,且
,0)两点,且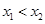 ,与
,与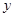 轴交于点
轴交于点 ,其中
,其中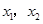 是方程
是方程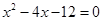 的两个根。(14分)
的两个根。(14分)
(1)求抛物线的解析式;
 (2)点
(2)点 是线段
是线段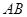 上的一个动点,过点
上的一个动点,过点 作
作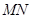 ∥
∥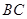 ,交
,交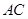 于点
于点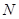 ,连接
,连接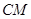 ,当
,当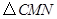 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标;
(3)点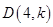 在(1)中抛物线上,
在(1)中抛物线上,
点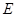 为抛物线上一动点,在
为抛物线上一动点,在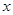 轴上是
轴上是
否存在点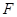 ,使以
,使以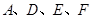 为顶
为顶
点的四边形是平行四边形,如果存在,
求出所有满足条件的点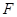 的坐标,
的坐标,
若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com