
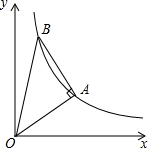
 如图,等腰Rt△OAB中∠OAB=90°,顶点O为坐标原点,顶点A、B在某反比例函数的图象上,点A的横坐标为2,则S△OAB=________.
如图,等腰Rt△OAB中∠OAB=90°,顶点O为坐标原点,顶点A、B在某反比例函数的图象上,点A的横坐标为2,则S△OAB=________.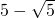
 )=4+k,再利用S△AOB=4+k-3×
)=4+k,再利用S△AOB=4+k-3× =4-
=4- ,进而利用AO=AB,再表示出即可得出S△AOB=
,进而利用AO=AB,再表示出即可得出S△AOB= ×
×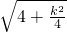 ×
×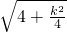 =2+
=2+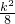 ,再利用两三角形面积相等得出k的值,即可得出答案.
,再利用两三角形面积相等得出k的值,即可得出答案.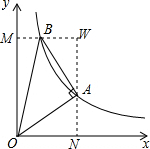 解:过点B作BM⊥y轴于点M,过点A作AN⊥x轴于点N,并延长MB,NA交于一点W,
解:过点B作BM⊥y轴于点M,过点A作AN⊥x轴于点N,并延长MB,NA交于一点W, ,
, ),
),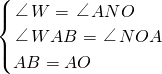 ,
, ,
, )=4+k,
)=4+k, ×2×
×2× =
= ,
, =4-
=4- ,
, ,
,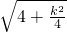 ,
, ×
×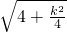 ×
×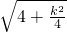 =2+
=2+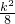 ,
, =2+
=2+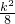 ,
, ,k2=-2-2
,k2=-2-2 (不合题意舍去),
(不合题意舍去), =4-
=4-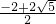 =5-
=5- .
. .
.

科目:初中数学 来源: 题型:
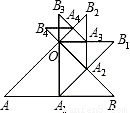
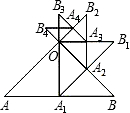 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是查看答案和解析>>
科目:初中数学 来源: 题型:
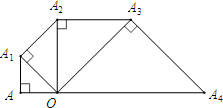 如图,等腰Rt△OAA1的直角边OA长为1.
如图,等腰Rt△OAA1的直角边OA长为1.| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年江苏省无锡市滨湖中学中考数学模拟试卷(二)(解析版) 题型:填空题
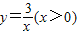 的图象上,连接OA,则OC2-OA2= .
的图象上,连接OA,则OC2-OA2= .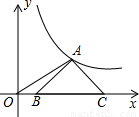
查看答案和解析>>
科目:初中数学 来源:2009年福建省泉州市晋江市初中学业质量检查数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com