

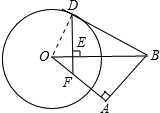
 解:(1)∵E、B两点及A、F两点分别为⊙O的互为反演点,
解:(1)∵E、B两点及A、F两点分别为⊙O的互为反演点,| OE |
| OA |
| OF |
| OB |
| R |
| EO |
| BO |
| R |


科目:初中数学 来源: 题型:
 能用一句话归纳你的发现吗?
能用一句话归纳你的发现吗?| 25 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| m |
| 2πr |
| m |
| 2πr |
| R+r |
| r |
| R+r |
| r |
| R-r |
| r |
| R-r |
| r |
查看答案和解析>>
科目:初中数学 来源:2009年江苏省淮安市金湖县外国语学校中考数学二模试卷(解析版) 题型:解答题
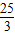 ,求PC、PD的长.
,求PC、PD的长.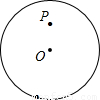
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com