
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值,对于任意正实数a、b,可作如下变形a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ,又∵
,又∵![]() ≥0,∴
≥0,∴ ![]() +2
+2![]() ≥0+ 2
≥0+ 2![]() ,即a+b ≥2
,即a+b ≥2![]() .
.
(1)根据上述内容,回答下列问题:在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥ 2
(a、b均为正实数)中,若ab为定值p,则a+b≥ 2![]() ,当且仅当a、b满足________时,a+b有最小值2
,当且仅当a、b满足________时,a+b有最小值2![]() .
.
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a ,DB=2b, 试根据图形验证a+b≥2![]() 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
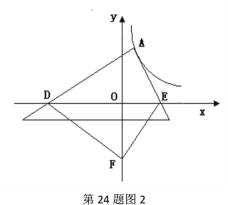
(3)探索应用:如图2,已知A为反比例函数![]() 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.

【答案】(1)a=b ;(2)当D与O重合时或a=b时,等式成立;(3)28.
【解析】
(1)由给出的材料可知a=b时;
(2)因为AD=2a,DB=2b,所以AB=2a+2b,CO为中线,所以CO=a+b,再利用射影定理得CD=![]() ,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
(3)把A点的横坐标为1,代入函数y=![]() 得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=
得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=![]() ×8×(4+3)=28.
×8×(4+3)=28.
(1)a=b,
(2)有已知得CO=a+b,CD=2![]() ,CO≥CD,即
,CO≥CD,即![]() ≥2
≥2![]() .
.
当D与O重合时或a=b时,等式成立.
(3)![]() ,
,
当DE最小时S四边形ADFE最小.
过A作AH⊥x轴,由(2)知:当DH=EH时,DE最小,
所以DE最小值为8,此时S四边形ADFE=![]() (4+3)=28.
(4+3)=28.


科目:初中数学 来源: 题型:
【题目】如图,点P是AOB内任意一点,OP=10cm,点P与点![]() 关于射线OA对称,点P与点
关于射线OA对称,点P与点![]() 关于射线OB对称,连接
关于射线OB对称,连接![]() 交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。
交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社为吸引市民组团去天水湾风景区旅游,推出如下收费标准:
![]() 如果人数不超过
如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元;
元;
![]() 如果人数超过
如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
某单位共付给该旅行社旅游费用![]() 元,问:该单位这次共有多少员工去天水湾风景区旅游?
元,问:该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,且
,且![]() 满足
满足![]() ,
,![]() 的坐标为
的坐标为![]()
(1)判断![]() 的形状.
的形状.
(2)动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/
个单位/![]() 的速度在线段
的速度在线段![]() 上运动,另一动点
上运动,另一动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/
个单位/![]() 的速度在射线
的速度在射线![]() 上运动,运动时间为
上运动,运动时间为![]() .
.
①如图2,若![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
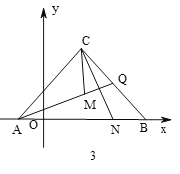
②如图3,若![]() ,当
,当![]() 运动到
运动到![]() 中点时,
中点时,![]() 为
为![]() 上一点,连
上一点,连![]() ,作
,作![]() 交
交![]() 于
于![]() .试探究
.试探究![]() 和
和![]() 的数量关系,并给出证明.
的数量关系,并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com