
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“伴随点”.
,那么称点Q为点P的“伴随点”.
例如:点(5,6)的“伴随点”为点(5,6);点(﹣5,6)的“伴随点”为点(﹣5,﹣6).
(1)直接写出点A(2,1)的“伴随点”A′的坐标.
(2)点B(m,m+1)在函数y=kx+3的图象上,若其“伴随点”B′的纵坐标为2,求函数y=kx+3的解析式.
(3)点C、D在函数y=﹣x2+4的图象上,且点C、D关于y轴对称,点D的“伴随点”为D′.若点C在第一象限,且CD=DD′,求此时“伴随点”D′的横坐标.
(4)点E在函数y=﹣x2+n(﹣1≤x≤2)的图象上,若其“伴随点”E′的纵坐标y′的最大值为m(1≤m≤3),直接写出实数n的取值范围.
【答案】(1)A'的坐标为(2,1);(2)①当m≥0时,y=﹣x+3;②m<0时,y=![]() x+3;(3)D′的横坐标为
x+3;(3)D′的横坐标为![]() ;(4)﹣2≤n≤0、1≤n≤3.
;(4)﹣2≤n≤0、1≤n≤3.
【解析】
(1)由题意即可求解;
(2)分m≥0、m<0两种情况分别求解即可;
(3)设点C的横坐标为n,点C在函数y=﹣x2+4的图象上,CD=DD′,即可求解;
(4)通过画图即可求解.
解:(1)由题意得:点A'的坐标为(2,1)
(2)①当m≥0时,
m+1=2,m=1
∴B(1,2)
∵点B在一次函数y=kx图象上,
∴k+3=2,
解得:k=+1
∴一次函数解析式为y=﹣x+3
②m<0时,
m+1=﹣2,m=﹣3
∴B(﹣3,﹣2)
∵点B在一次函数y=kx+3图象上,
∴﹣3k+3=﹣2
解得:k=![]()
一次函数解析式为y=![]() x+3.
x+3.
(3)设点C的横坐标为n,点C在函数y=﹣x2+4的图象上,
∴点C的坐标为(n,﹣n2+4),
∴点D的坐标为(﹣n,﹣n2+4),D′(﹣n,n2﹣4)
∵CD=DD′,
∴2n=2(n2+4),
解得:n=![]() ;
;
∵点C在第一象限,
∴D′的横坐标为![]() ;
;
(4)﹣2≤n≤0、1≤n≤3,
当左边的抛物线在上方时,如图①、图②:﹣2≤n≤0;
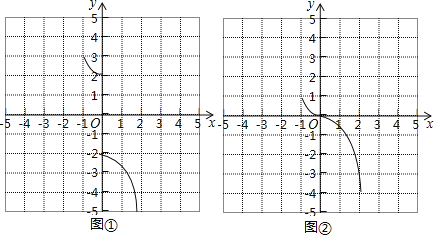
当右边的抛物线在上方时,如图③、图④:1≤n≤3.



科目:初中数学 来源: 题型:
【题目】“重整行装再出发,驰而不息再争创”,2018年5月8日兰州市召开了新一轮全国文明城市创建启动大会.某校为了更好地贯彻落实创建全国文明城市目标,举办了“我是创城小主人”的知识竞赛.该校七年级、八年级分别有300人,现从中各随机抽取10名同学的测试成绩进行调查分析,成绩如下:
七年级 | 85 | 65 | 84 | 78 | 100 | 78 | 85 | 85 | 98 | 83 |
八年级 | 96 | 60 | 87 | 78 | 87 | 87 | 89 | 100 | 83 | 96 |
整理、描述数据:
分数段 |
|
|
|
|
七年级人数 | 1 | 2 | 5 | 2 |
八年级人数 | 1 | 1 | 5 | 3 |
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七 | 84.1 | _______ | 85 |
八 | 86.3 | 87 | ______ |
得出结论:
(1)根据上述数据,将表格补充完整;
(2)估计该校七、八两个年级学生在本次测试成绩中可以取得优秀的人数![]() 共有多少人?
共有多少人?
(3)你认为哪个年级知识掌握的总体水平较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
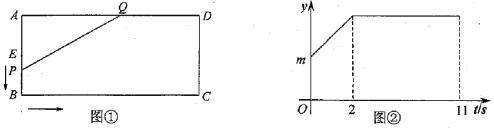
【题目】如图①,在矩形![]() 中,点
中,点![]() 从
从![]() 边的中点
边的中点![]() 出发,沿着
出发,沿着![]() 速运动,速度为每秒2个单位长度,到达点
速运动,速度为每秒2个单位长度,到达点![]() 后停止运动,点
后停止运动,点![]() 是
是![]() 上的点,
上的点,![]() ,设
,设![]() 的面积为
的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() 秒,
秒,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
(1)图①中![]() = ,
= ,![]() = ,图②中
= ,图②中![]() = .
= .
(2)当![]() =1秒时,试判断以
=1秒时,试判断以![]() 为直径的圆是否与
为直径的圆是否与![]() 边相切?请说明理由:
边相切?请说明理由:
(3)点![]() 在运动过程中,将矩形沿
在运动过程中,将矩形沿![]() 所在直线折叠,则
所在直线折叠,则![]() 为何值时,折叠后顶点
为何值时,折叠后顶点![]() 的对应点
的对应点![]() 落在矩形的一边上.
落在矩形的一边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
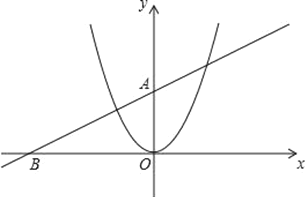
【题目】已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.
(1)求直线的解析式;
(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;
(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
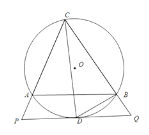
【题目】如图,△ABC内接于圆O,CD平分∠ACB交于圆O,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是圆O的切线;
(2)连接AD,求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com