
已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上的点,且满足
是抛物线上的点,且满足![]() ∥
∥![]() 轴,点
轴,点![]() 是抛物线的顶点.
是抛物线的顶点.

(1)求抛物线的对称轴及![]() 点坐标;
点坐标;
(2)若抛物线经过点![]() ,求抛物线的表达式;
,求抛物线的表达式;
(3)对(2)中的抛物线,点![]() 在线段
在线段![]() 上,若以点
上,若以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,试求点
相似,试求点![]() 的坐标.
的坐标.
(1)![]()
(2)![]()
(3)点![]() 的坐标为
的坐标为![]() 或
或
解析:解(1)由题意得,![]() ,∴对称轴为直线
,∴对称轴为直线![]() ;…………………(2分)
;…………………(2分)
∵点![]() ,点
,点![]() 是抛物线上的点,
是抛物线上的点,![]() ∥
∥![]() 轴,
轴,
∴![]() 被直线
被直线![]() 垂直平分,∴
垂直平分,∴![]() .………………………………………(1分)
.………………………………………(1分)
(2)∵抛物线经过点![]() ,
,![]() ,所以有
,所以有![]() ,……………(2分)
,……………(2分)
解得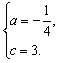 ,∴抛物线的表达式为
,∴抛物线的表达式为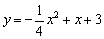 .………………………(1分)
.………………………(1分)
(3)∵抛物线的对称轴为直线![]() ,∴
,∴![]() ,…………………………(1分)
,…………………………(1分)
过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,设对称轴与
,设对称轴与![]() 交于点
交于点![]() .……………(1分)
.……………(1分)
∵![]() ∥
∥![]() 轴,∴
轴,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ∽
∽![]() ,…………(1分)
,…………(1分)
∴![]() ,………………………………………………………………(1分)
,………………………………………………………………(1分)
当![]() ∽
∽![]() 时,有
时,有![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ;…………………(1分)
;…………………(1分)
当![]() ∽
∽![]() 时,有
时,有![]() ,
,
∴![]() ,∴
,∴![]() ,………………………………………………………(1分)
,………………………………………………………(1分)
综上所述满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,顶点为
,顶点为![]() .
.
(Ⅰ)若![]() ,
,![]() ,求此时抛物线顶点
,求此时抛物线顶点![]() 的坐标;
的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线![]() 的解析式;
的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点![]() 恰好落在直线
恰好落在直线![]() 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线与![]() 轴交于点
轴交于点![]() ,
,![]() ,与y轴交于点
,与y轴交于点![]() .
.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交![]() 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
 与
与 轴交于点
轴交于点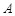 (-1,0)、
(-1,0)、 (3,0),与
(3,0),与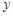 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为 .
.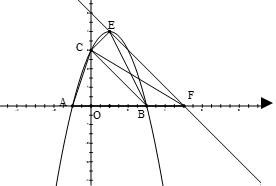
 的坐标;
的坐标; 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: . 轴交于点M、N,与
轴交于点M、N,与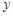 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式查看答案和解析>>
科目:初中数学 来源: 题型:
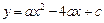 与
与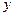 轴交于点
轴交于点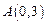 ,点
,点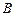 是抛物线上的点,且满足
是抛物线上的点,且满足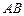 ∥
∥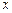 轴,点
轴,点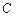 是抛物线的顶点.
是抛物线的顶点.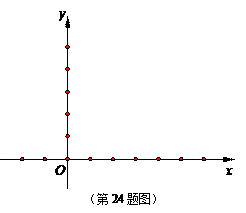
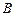 点坐标;
点坐标;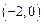 ,求抛物线的表达式;
,求抛物线的表达式;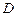 在线段
在线段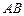 上,若以点
上,若以点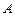 、
、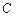 、
、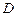 为顶点的三角形与
为顶点的三角形与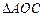 相似,试求点
相似,试求点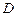 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
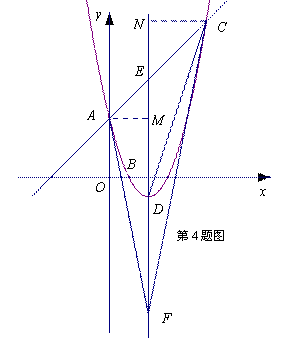
如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com