
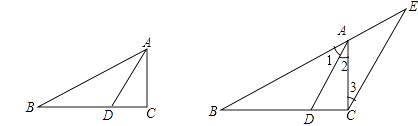
【题目】如图①,在Rt△ABC中,∠C=90°.将△ABC绕点C逆时针旋转得到△A’B’C,旋转角为 ![]() ,且0°<
,且0°< ![]() <180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
<180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
(1)求∠A的度数;
(2)当点C到AA’的距离等于AC的一半时,求 ![]() 的度数.
的度数.
【答案】
(1)解:将 ![]() 绕点
绕点 ![]() 逆时针旋转得到
逆时针旋转得到 ![]() ,旋转角为
,旋转角为 ![]() ,
,
∴ ![]() .
.
∵点 ![]() 可以恰好落在
可以恰好落在 ![]() 的中点处,
的中点处,
∴点 ![]() 是
是 ![]() 的中点.
的中点.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
即 ![]() 是等边三角形.
是等边三角形.
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]()
(2)解:如图,过点 ![]() 作
作 ![]() 于点
于点 ![]() ,
,

点 ![]() 到
到 ![]() 的距离等于
的距离等于 ![]() 的一半,即
的一半,即 ![]() .
.
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() ,即
,即 ![]() .
.
【解析】(1)由旋转性质和直角三角形的斜边中线性质,可先得∠ B = 60 °,再推出∠ A = 30 °;(2)利用30度角的正弦函数,先求出∠ C A D = 30 °,再求出旋转角∠ A C A ' = 120 ° .
【考点精析】利用锐角三角函数的定义和旋转的性质对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.
(1)求证:△ACD∽△ABC;
(2)若AD=6,AB=10,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中, AD是角平分线.
求证: ![]() .
.
证明:过C作CE∥DA,交BA的延长线于E.
∴ ![]() . ①
. ①![]() AD是角平分线,
AD是角平分线,
∴ ![]() .
.![]()
![]() .
.![]() . ②
. ②
又 ![]() ,
,![]() . ③
. ③![]()
![]() .
.
(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,求BD的长;
(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△ABD和△ACD面积的比来证明三角形内角平分线定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.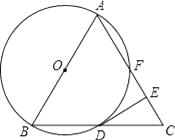
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直径为 ![]() 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0, ![]() ).
).
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象的顶点坐标为(1, ![]() ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
(1)求该二次函数的表达式;
(2)判断点B是否在此二次函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
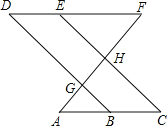
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若![]() ,
,![]() .
.
求证:![]() .
.
证明:![]()
![]() ______
______![]() 对顶角相等
对顶角相等![]()
![]() ,
,
![]() ______
______![]()
![]() ______
______![]() ______
______![]()
又![]()
![]() ,
,
![]() ______
______![]() ______
______![]()
![]() ______
______![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com