
 如图,正方形ABCO的边长为
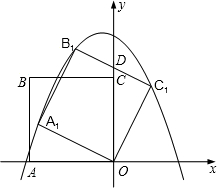
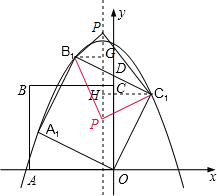
如图,正方形ABCO的边长为 ,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1. 个单位长度的速度沿射线A1O下滑,直至顶点B1落在x轴上时停止.设正方形落在x轴上方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
个单位长度的速度沿射线A1O下滑,直至顶点B1落在x轴上时停止.设正方形落在x轴上方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.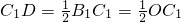 .
.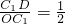 .
. .
. ②过点A1作A1E⊥x轴,垂足为点E.
②过点A1作A1E⊥x轴,垂足为点E.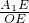 ,
,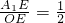 .
. ,
,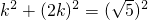 ,
,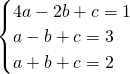

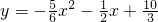 .
. (2)将(1)的抛物线解析式配方,得
(2)将(1)的抛物线解析式配方,得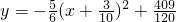 .
. .
. 时,y=2×(-
时,y=2×(- )+5=
)+5= ;
; 时,y=2×(-
时,y=2×(- )=-
)=- ;
; ,y):
,y): =
= 、PG=y-3、C1H=1+
、PG=y-3、C1H=1+ =
= 、PH=y-2
、PH=y-2
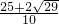 、y=
、y=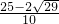 (舍);
(舍);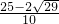 ;
;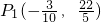 ,
,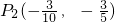 ,
, ,
,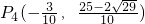 .
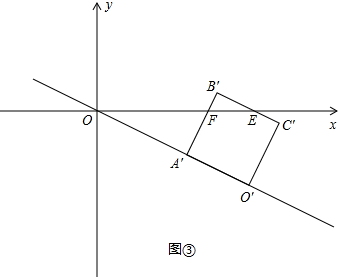
. (3)设运动后的正方形为O′A′B′C′,分三种情况:
(3)设运动后的正方形为O′A′B′C′,分三种情况: ;
; 时,如图①;
时,如图①; t,O′E=
t,O′E= OO′=
OO′= t
t ×2
×2 t×
t× t=-5t2+5;
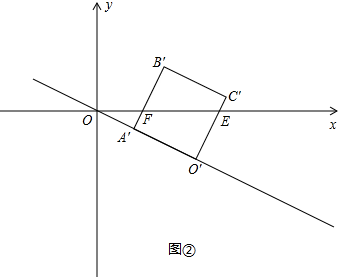
t=-5t2+5; <t<1时,如图②;
<t<1时,如图②; t,OA′=2
t,OA′=2 t-
t- ,A′F=
,A′F= OA′=
OA′=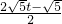 ,O′E=
,O′E= OO′=
OO′= t
t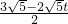 ,C′E=O′C′-O′E=
,C′E=O′C′-O′E= -
- t;
t; (B′F+C′E)×B′C′=
(B′F+C′E)×B′C′= (
(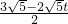 +
+ -
- t)×
t)× =
=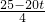 ;
; ;
; 时,如图③;
时,如图③;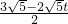 ,B′E=2B′F=3
,B′E=2B′F=3 -2
-2 t;
t; ×
×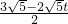 ×(3
×(3 -2
-2 t)=5t2-15t+
t)=5t2-15t+ ;
;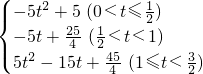 .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
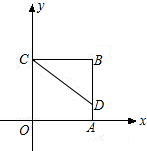 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
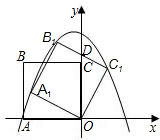 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
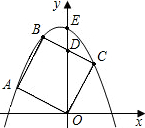 x2+bx+c经过B、C且与y轴的交点为E(0,
x2+bx+c经过B、C且与y轴的交点为E(0,| 10 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com