
【题目】如图![]() ,已知抛物线
,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为顶点.
为顶点.
![]() 求直线
求直线![]() 的解析式和顶点
的解析式和顶点![]() 的坐标;
的坐标;
![]() 已知
已知![]() ,点
,点![]() 是直线
是直线![]() 下方的抛物线上一动点,作
下方的抛物线上一动点,作![]() 于点
于点![]() ,当
,当![]() 最大时,有一条长为
最大时,有一条长为![]() 的线段
的线段![]() (点
(点![]() 在点
在点![]() 的左侧)在直线
的左侧)在直线![]() 上移动,首尾顺次连接
上移动,首尾顺次连接![]() 、
、![]() 、
、![]() 、
、![]() 构成四边形
构成四边形![]() ,请求出四边形
,请求出四边形![]() 的周长最小时点
的周长最小时点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 点是线段
点是线段![]() 上一动点,将
上一动点,将![]() 沿直线
沿直线![]() 折叠至
折叠至![]() ,是否存在点
,是否存在点![]() 使得
使得![]() 与
与![]() 重叠部分的图形是直角三角形?若存在,请求出
重叠部分的图形是直角三角形?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
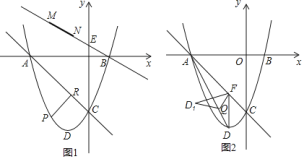
【答案】![]() 直线
直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 坐标
坐标![]() .
.![]()
![]() .
.![]() 存在.当
存在.当![]() 与
与![]() 重叠部分的图形是直角三角形时,
重叠部分的图形是直角三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分别令x=0和y=0可求解出ABC三点的坐标,利用待定系数法求解直线AC的解析式;将二次函数一般式化为顶点式即可求解D点坐标;
(2)由于AC长度固定,故当PR最大时,△APC的面积最大,由图像可知![]() ,设P(m,m2+2m-3),代入其中可求解m从而确定P点坐标;将点
,设P(m,m2+2m-3),代入其中可求解m从而确定P点坐标;将点![]() 沿
沿![]() 方向平移
方向平移![]() 个单位得到
个单位得到![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,此时四边形
,此时四边形![]() 的最长最小;
的最长最小;
(3)分三种情况进行讨论:当![]() 时,重叠部分是RT△FKQ;当
时,重叠部分是RT△FKQ;当![]() 时,重叠部分是RT△FQD;、当
时,重叠部分是RT△FQD;、当![]() 时,重叠部分是RT△QMF.
时,重叠部分是RT△QMF.
![]() 对于抛物线
对于抛物线![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,
∴![]() ,
,
∵抛物线![]() ,
,
∴顶点![]() 坐标为
坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,则有
,则有![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 坐标
坐标![]() .
.
![]() 如图
如图![]() 中,设
中,设![]()

由题意,当![]() 最大时,
最大时,![]() 的面积最大,即四边形
的面积最大,即四边形![]() 的面积最大,
的面积最大,
∵
![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 的面积最大,即
的面积最大,即![]() 最长,
最长,
∴![]() ,
,
将点![]() 沿
沿![]() 方向平移
方向平移![]() 个单位得到
个单位得到![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,此时四边形
,此时四边形![]() 的最长最小,
的最长最小,
∵直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
由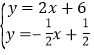 解得
解得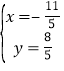 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由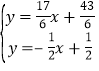 解得
解得 ,
,
∴![]() ,将点
,将点![]() 向下平移
向下平移![]() 个单位,向右平移
个单位,向右平移![]() 个单位得到
个单位得到![]() ,
,
∴![]() .
.
![]() 存在.
存在.
①如图![]() 中,当
中,当![]() 时,重叠部分是
时,重叠部分是![]() ,作
,作![]() 于
于![]() .
.
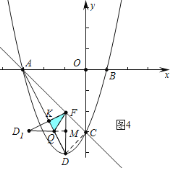
由题意可求得![]() ,容易求得
,容易求得![]() ,
,![]() ,
,![]() ,
,![]() ,CD=
,CD=![]()
∵AD2=20=AC2+CD2,
∴∠ACD=90°,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,设
,设![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()
②如图![]() 中,当
中,当![]() 时,重叠部分是
时,重叠部分是![]() ,此时
,此时![]() .
.
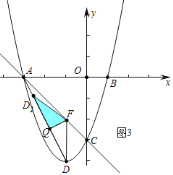
③如图![]() 中,当
中,当![]() 时,重叠部分是
时,重叠部分是![]() .
.
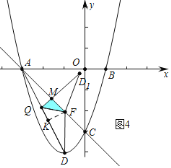
设![]() ,在
,在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,当![]() 与
与![]() 重叠部分的图形是直角三角形时,
重叠部分的图形是直角三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
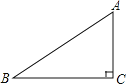
(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.
(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,
(1)求这两个函数表达式
(2)写出使反比例函数值大于一次函数值时![]() 的取值范围。
的取值范围。
(3)△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
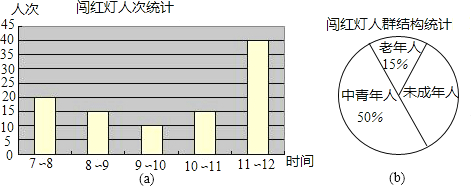
【题目】在“不闯红灯,珍惜生命”活动中,文明中学的王欣和李好两位同学某天来到城区中心的十字路口,观察、统计上午7:![]() :00中闯红灯的人次,制作了两个数据统计图
:00中闯红灯的人次,制作了两个数据统计图![]() 图
图![]() 和
和![]() .
.
![]() 图a提供的五个数据
图a提供的五个数据![]() 各时段闯红灯人次
各时段闯红灯人次![]() 的中位数是______,平均数是______;
的中位数是______,平均数是______;
![]() 在扇形统计图中,求未成年人类对应扇形的圆心角的度数,并估计一个月
在扇形统计图中,求未成年人类对应扇形的圆心角的度数,并估计一个月![]() 按30天计算
按30天计算![]() 上午7:
上午7:![]() :00在该十字路口闯红灯的未成年人约有多少人次.
:00在该十字路口闯红灯的未成年人约有多少人次.
![]() 根据统计图提供的信息向交通管理部门提出一条合理化建议.
根据统计图提供的信息向交通管理部门提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践![]() 四边形旋转中的数学
四边形旋转中的数学
“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解答.
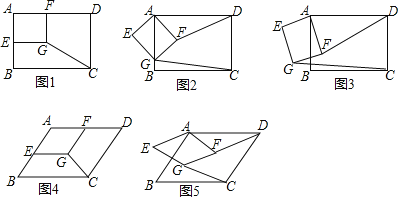
任务一:如图1,在矩形ABCD中,![]() ,
,![]() ,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
![]() 请直接写出CG的长是______.
请直接写出CG的长是______.
![]() 如图2,当矩形AEGF绕点A旋转
如图2,当矩形AEGF绕点A旋转![]() 比如顺时针旋转
比如顺时针旋转![]() 至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
![]() 当矩形AEGF绕点A旋转至如图3的位置时,
当矩形AEGF绕点A旋转至如图3的位置时,![]() 中DF与CG之间的数量关系是否还成立?请说明理由.
中DF与CG之间的数量关系是否还成立?请说明理由.
任务二:“智慧”数学小组对图形的旋转进行了拓展研究,如图4,在ABCD中,![]() ,
,![]() ,
,![]() ,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接
,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接![]() “智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
“智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
![]() 如图5,当AEGF绕点A旋转
如图5,当AEGF绕点A旋转![]() 比如顺时针旋转
比如顺时针旋转![]() ,其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系
,其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系![]() 请你直接写出这个特定的数量关系.
请你直接写出这个特定的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,已知![]() 的三个顶点在格点上.
的三个顶点在格点上.
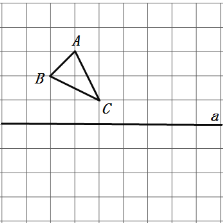
(1)以![]() 为顶点,画一个
为顶点,画一个![]() ,使
,使![]() 三边长分别为2,
三边长分别为2,![]() ,
,![]() ;
;
(2)画出![]() ,使它与
,使它与![]() 关于直线
关于直线![]() 对称;
对称;
(3)写出![]() 的面积,即
的面积,即![]() ______;
______;
(4)在直线![]() 上画出点
上画出点![]() ,使
,使![]() 最小,最小值为______.
最小,最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).
).
(1)![]() _____,点A的坐标为______,点B的坐标为_____;
_____,点A的坐标为______,点B的坐标为_____;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MAN=60°,点B在射线AM上,AB=4(如图).P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心.
(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;



(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC﹒AO=y,求y关于x的函数解析式,并写出自变量的取值范围;
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]()
![]() 如图①,求证:
如图①,求证:![]() ;
;
![]() 如图②,将
如图②,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .连接
.连接![]() .
.
①若![]() ,求
,求![]() 的长;
的长;
②若![]() ,在图②的旋转过程中,当
,在图②的旋转过程中,当![]() 时,直接写出旋转角
时,直接写出旋转角![]() 的大小.
的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com