
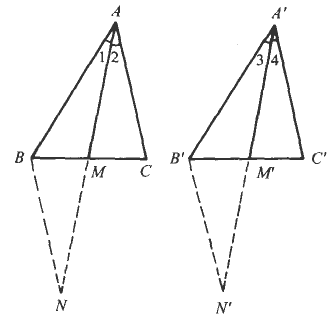
求证:如果两个三角形的两条边和第三边上的中线对应相等,那么这两个三角形全等.
已知:如图,在△ABC和△![]() 中,AB=
中,AB=![]() ,AC=
,AC=![]() ,M是BC中点,
,M是BC中点,![]() 是
是![]() 中点,且AM=
中点,且AM=![]() .
.
求证:△ABC≌△![]() .
.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
 .
.查看答案和解析>>
科目:初中数学 来源: 题型:
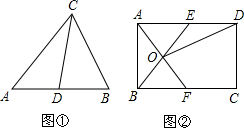 (2013•沈阳)定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
(2013•沈阳)定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠 同步讲解 九年级数学(下) 华东师大版 题型:044
下面的证明过程,看是否有错,若有错,指出错误的地方.(说明理由),并加以改正,(写出正确的证明过程).
求证:如果两个三角形中,有两边和其中一边上的中线对应相等,那么这两个三角形全等.
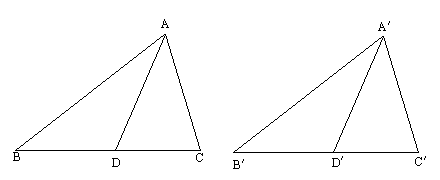
已知:如图,AD、![]() 分别是△ABC和△
分别是△ABC和△![]() 的中线,且AB=
的中线,且AB=![]() ,BC=
,BC=![]() ,AD=
,AD=![]() 求证:△ABC≌△
求证:△ABC≌△![]()
证明:∵BD=![]() BC,
BC,![]() =
=![]()
![]() ,BD=
,BD=![]()
∴在△ABC与△![]() 中
中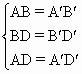 ,∴△ABD≌△
,∴△ABD≌△![]()
![]() (SSS)
(SSS)
同理:△ADC≌△![]() (SSS),∴△ABD+△ADC≌△
(SSS),∴△ABD+△ADC≌△![]()
![]() +△
+△![]() ,即△ABC≌△
,即△ABC≌△![]()
查看答案和解析>>
科目:初中数学 来源:新课标教材导学 数学九年级(第一学期) 题型:047
证明题
求证:如果两个三角形有两条边和其中一边上的中线分别对应相等,那么这两个三角形全等.(提示:首先分清题设和结论,画出图形,再结合图形写出“已知”、“求证”、“证明”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com