
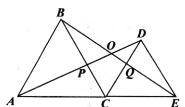
【题目】如图,点![]() 为线段
为线段![]() 上一点,在
上一点,在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和
和![]() ,
,![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,以下结论:①
,以下结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .以上结论正确的有_________(把你认为正确的序号都填上).
.以上结论正确的有_________(把你认为正确的序号都填上).
【答案】①②④
【解析】
根据等边三角形的性质可得CA=CB,CD=CE,∠ACB=∠DCE=60°,然后根据等式的基本性质可得∠ACD=∠BCE,利用SAS即可证出![]() ≌
≌![]() ,即可判断①;根据全等三角形的性质,即可判断②;利用三角形的内角和定理和等量代换即可求出∠AOB,即可判断③,最后利用ASA证出
,即可判断①;根据全等三角形的性质,即可判断②;利用三角形的内角和定理和等量代换即可求出∠AOB,即可判断③,最后利用ASA证出![]() ≌
≌![]() ,即可判断④.
,即可判断④.
解:∵△ABC和△CDE都是等边三角形
∴CA=CB,CD=CE,∠ACB=∠DCE=60°
∴∠ACB+∠BCD=∠DCE+∠BCD
∴∠ACD=∠BCE
在![]() 和
和![]() 中
中
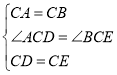
∴![]() ≌
≌![]() ,故①正确;
,故①正确;
∴∠CAD=∠CBE,![]() ,故②正确;
,故②正确;
∵∠OPB=∠CPA
∴∠AOB=180°-∠OPB-∠CBE=180°-∠CPA-∠CAD=∠ACB=60°,故③错误;
∵∠BCQ=180°-∠ACB-∠DCE=60°
∴∠ACP=∠BCQ
在![]() 和
和![]() 中
中
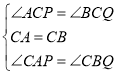
∴![]() ≌
≌![]() ,
,
∴![]() ,故④正确.
,故④正确.
故答案为:①②④.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE=60°.其中正确的结论个数为( )
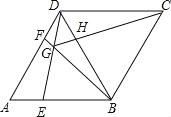
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() 的解析式为
的解析式为![]() ,直线
,直线 ![]() 的解析式为
的解析式为![]() ,
,![]() 为
为![]() 上的一点,且
上的一点,且![]() 点的坐标为
点的坐标为![]() 作直线
作直线 ![]() 轴,交直线于
轴,交直线于![]() 点
点![]() ,再作
,再作![]() 于点
于点![]() ,交直线
,交直线 ![]() 于点
于点![]() ,作
,作![]() 轴,交直线于
轴,交直线于![]() 点
点![]() ,再作
,再作![]()
![]() 于点
于点![]() ,作
,作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ....按此作法继续作下去,则
....按此作法继续作下去,则 ![]() 的坐标为_____,
的坐标为_____,![]() 的坐标为______
的坐标为______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
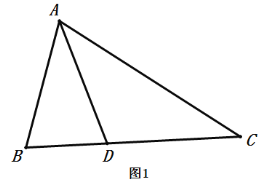
如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() .求证:
.求证:![]()
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
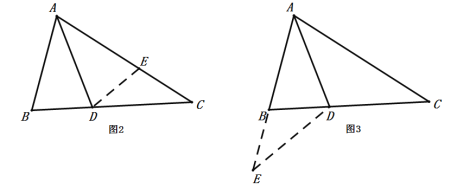
方法1:如图2,在![]() 上截取
上截取![]() ,使得
,使得![]() ,连接
,连接![]() ,可以得到全等三角形,进而解决问题
,可以得到全等三角形,进而解决问题
方法二:如图3,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,可以得到等腰三角形,进而解决问题
,可以得到等腰三角形,进而解决问题
(1)根据阅读材料,任选一种方法证明![]()
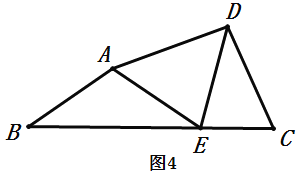
(2)根据自己的解题经验或参考小明的方法,解决下面的问题:如图4,四边形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() ,探究
,探究![]() 、
、![]() 、
、![]() 之间的数量关系,并证明
之间的数量关系,并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
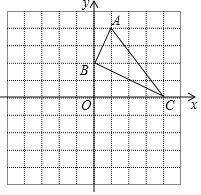
【题目】如图,已知网格上最小的正方形的边长为![]() (长度单位),点
(长度单位),点![]() 在格点上.
在格点上.
(1)直接在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() (点
(点![]() 对应点
对应点![]() ,点
,点![]() 对应点
对应点![]() );
);
(2)![]() 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);
(3)点![]() 到直线
到直线![]() 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是反比例函数![]() 的图象的一支.根据给出的图象回答下列问题:
的图象的一支.根据给出的图象回答下列问题:
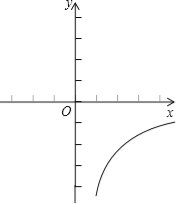
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com