
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,而
的小数部分我们不可能全部写出来,而![]() <2于是可用
<2于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是_______,小数部分是_________;
的整数部分是_______,小数部分是_________;
(2)如果![]() 的小数部分为
的小数部分为![]() 的整数部分为
的整数部分为![]() 求
求![]() 的值;
的值;
(3)已知:![]() 其中
其中![]() 是整数,且
是整数,且![]() 求
求![]() 的平方根。
的平方根。
【答案】(1) 4,![]() -4;(2)1;(2) ±12.
-4;(2)1;(2) ±12.
【解析】
(1)先估算出![]() 的范围,即可得出答案;
的范围,即可得出答案;
(2)先估算出![]() 、
、![]() 的范围,求出a、b的值,再代入求出即可;
的范围,求出a、b的值,再代入求出即可;
(3)先估算出![]() 的范围,求出x、y的值,再代入求出即可.
的范围,求出x、y的值,再代入求出即可.
解:(1)∵4<![]() <5,
<5,
∴![]() 的整数部分是4,小数部分是
的整数部分是4,小数部分是![]() -4,
-4,
故答案为:4,![]() -4;
-4;
(2)∵2<![]() <3,
<3,
∴a=![]() -2,
-2,
∵3<![]() <4,
<4,
∴b=3,
∴a+b-![]() =
=![]() -2+3-
-2+3-![]() =1;
=1;
(3)∵100<110<121,
∴10<![]() <11,
<11,
∴110<100+![]() <111,
<111,
∵100+![]() =x+y,其中x是整数,且0<y<1,
=x+y,其中x是整数,且0<y<1,
∴x=110,y=100+![]() -110=
-110=![]() -10,
-10,
∴x+![]() +24-y=110+
+24-y=110+![]() +24-
+24-![]() +10=144,
+10=144,
x+![]() +24-y的平方根是±12.
+24-y的平方根是±12.


科目:初中数学 来源: 题型:
【题目】某学校举行数学竞赛,需购买![]() 两种奖品共160件,其中
两种奖品共160件,其中![]() 种奖品的单价为12元,
种奖品的单价为12元,![]() 种奖品的单价为8元,且购买
种奖品的单价为8元,且购买![]() 种奖品的数量不大于
种奖品的数量不大于![]() 种奖品数量的3倍,假设购买
种奖品数量的3倍,假设购买![]() 种奖品的数量为
种奖品的数量为![]() 件.
件.
(1)根据题意填空:
购买![]() 种奖品的费用为___(元);
种奖品的费用为___(元);
购买![]() 种奖品的费用为___(元);
种奖品的费用为___(元);
(2)若购买两种奖品所需的总费用为![]() 元,试求
元,试求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(3)问![]() 两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
图书类别 | 画记 | 人数 | 百分比 | ||
文学类 | |||||
艺体类 | 正 | 5 | |||
科普类 | |||||
其他 | 正正 | 14 | |||
合计 | a | 100% |
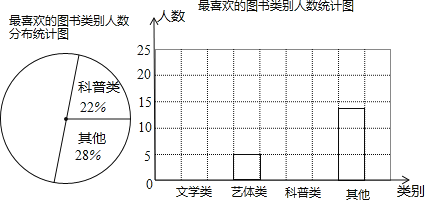
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量![]() 为________;
为________;
(2)在扇形统计图中,“艺体类”所在的扇形圆心角应等于_________度;
(3)补全条形统计图;
(4)已知该校有![]() 名学生,估计全校最喜欢文学类图书的学生有________人.
名学生,估计全校最喜欢文学类图书的学生有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)
(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由
(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;
(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在D处测得山顶C的仰角为37°,向前走100米来到山脚A处,测得山坡AC的坡度为i=1:0.5,求山的高度(不计测角仪的高度,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com