
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,
上,![]() ,连结
,连结![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点.
的中点.

(1)观察猜想图1中,线段![]() 与
与![]() 的数量关系是_______,位置关系是_______;
的数量关系是_______,位置关系是_______;
(2)探究证明把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,连结
逆时针方向旋转到图2的位置,连结![]() 、
、![]() 、
、![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 是等腰直角三角形,理由见解析;(3)
是等腰直角三角形,理由见解析;(3)![]() 面积的最大值为
面积的最大值为![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出
BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出![]() 得出
得出![]() ,最后用互余即可得出结论;
,最后用互余即可得出结论;
(2)先判断出![]() ,得出
,得出![]() ,同(1)的方法得出
,同(1)的方法得出![]() ,
,![]() ,即可得出
,即可得出![]() ,同(1)的方法即可得出结论;
,同(1)的方法即可得出结论;
(3)先判断出![]() 最大时,
最大时,![]() 的面积最大,进而求出
的面积最大,进而求出![]() ,
,![]() ,即可得出
,即可得出![]() ,最后用面积公式即可得出结论.
,最后用面积公式即可得出结论.
解:(1)∵点![]() 、
、![]() 是
是![]() 、
、![]() 的中点
的中点
∴![]() ,
,![]()
∵点![]() 、
、![]() 是
是![]() 、
、![]() 的中点
的中点
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
(2)结论:![]() 是等腰直角三角形.
是等腰直角三角形.
证明:由旋转知,![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∵由三角形中位线的性质可知,![]() ,
,![]()
∴![]()
∴![]() 是等腰三角形
是等腰三角形
∵同(1)的方法得,![]() 、
、![]()
同(1)的方法得, ![]() 、
、![]()
∴![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
∵![]()
∴![]()
∴![]()
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(3)∵由(2)得,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() 最大时,
最大时,![]() 的面积最大
的面积最大
∴![]() 且
且![]() 在顶点
在顶点![]() 上面时,
上面时,![]() ,连接AM,AN,如图:
,连接AM,AN,如图:
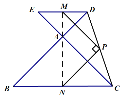
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]()
∴![]() .
.
故答案是:(1)![]() ,
,![]() ;(2)
;(2)![]() 是等腰直角三角形,理由见解析;(3)
是等腰直角三角形,理由见解析;(3)![]() 面积的最大值为
面积的最大值为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得到C2,C2与x轴交于点B、D,若直线y=
与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得到C2,C2与x轴交于点B、D,若直线y=![]() x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
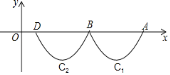
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳身高1.6米,此时太阳光线与地面的夹角为45°.
(1)若小芳正站在水平地面A处上时,那么她的影长为多少米?
(2)若小芳来到一个坡度i=![]() 的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?
的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?
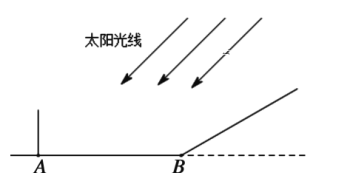
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“可控变点”.请问:若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的值是____.
,则称点Q为点P的“可控变点”.请问:若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;
(2)若在如图三个空格的右侧增加一个空格,将A、B、C、D四个字母任意填写其中(每空填一个字母,每空中的字母不重复),从左往右字母顺序恰好是A、B、C、D的概率为 .
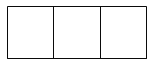
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
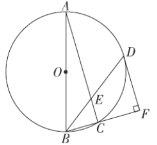
【题目】如图,AB是⊙O的直径,△ABC内接于⊙O.点D在⊙O 上,BD平分∠ABC交AC于点E,DF⊥BC交BC的延长线于点F.
(1)求证:FD是⊙O的切线;
(2)若BD=8,sin∠DBF=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当图形具有邻边相等的特征时,我们可以把图形的一部分绕着公共端点旋转,这样将分散的条件集中起来,从而达到解决问题的目的
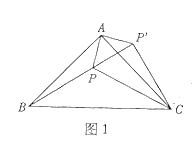
![]() 如图1,等腰直角三角形
如图1,等腰直角三角形![]() 内有一点
内有一点![]() 连接
连接![]() 为探究
为探究![]() 三条线段间的数量关系,我们可以将
三条线段间的数量关系,我们可以将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() 连接
连接![]() 则
则![]() ___ ____
___ ____![]() 是_ 三角形,
是_ 三角形,![]() 三条线段的数量关系是_ ;
三条线段的数量关系是_ ;
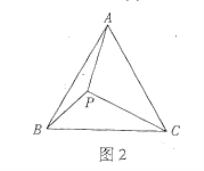
![]() 如图2,等边三角形
如图2,等边三角形![]() 内一点P,连接
内一点P,连接![]() 请借助第一问的方法探究
请借助第一问的方法探究![]() 三条线段间的数量关系.
三条线段间的数量关系.
![]() 如图3 ,在四边形
如图3 ,在四边形![]() 中,
中,![]() 点
点![]() 在四边形内部,且
在四边形内部,且![]()
![]() 请直接写出
请直接写出![]() 的长.
的长.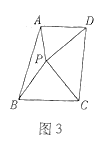
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com