
【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB

【答案】见解析;
【解析】
灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB.
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直的定义).


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上(
上(![]() ,
,![]() 除外),
除外),![]() 的垂线
的垂线![]() 与
与![]() 的垂线
的垂线![]() 交于点
交于点![]() ,研究
,研究![]() 和
和![]() 的数量关系.
的数量关系.
(1)在探究![]() ,
,![]() 的关系时,运用“从特殊到一般”的数学思想,发现当点
的关系时,运用“从特殊到一般”的数学思想,发现当点![]() 是
是![]() 的中点时,只需要取
的中点时,只需要取![]() 边的中点
边的中点![]() (如图),通过推理证明就可以得到
(如图),通过推理证明就可以得到![]() 的数量关系,请你按照这种思路直接写出
的数量关系,请你按照这种思路直接写出![]() 和
和![]() 的数量关系:_____________________
的数量关系:_____________________

(2)当点![]() 是线段
是线段![]() 上(
上(![]() ,
,![]() 除外)任意一点(其它条件不变),上面得到的结论是否仍然成立呢?证明你的结论;
除外)任意一点(其它条件不变),上面得到的结论是否仍然成立呢?证明你的结论;

(3)点![]() 在线段
在线段![]() 的延长线上,上面得到的结论是否仍然成立呢?在下图中画出图形,并证明你的结论.
的延长线上,上面得到的结论是否仍然成立呢?在下图中画出图形,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,⊙I为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8.
(1)求⊙I的半径;
(2)求线段OI的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 为正三角形,点
为正三角形,点![]() 、
、![]() 分别在菱形的边
分别在菱形的边![]() 、
、![]() 上滑动,且
上滑动,且![]() 、
、![]() 不与
不与![]() 、
、![]() 、
、![]() 重合.
重合.

(1)证明不论![]() 、
、![]() 在
在![]() 、
、![]() 上如何滑动,总有
上如何滑动,总有![]() ;
;
(2)当点![]() 、
、![]() 在
在![]() 、
、![]() 上滑动时,分别探讨四边形
上滑动时,分别探讨四边形![]() 和
和![]() 的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.
的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与时同的变化情况,如图所示.
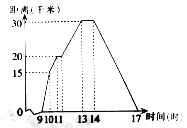
(1)图象表示了哪两个变量的关系?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时他行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 Rt△ABC 中,∠BAC=90°,AC=AB,点 F 是射线 CA 上一点,连接 BF,过 C 作 CE⊥BF,垂足为点 E,直线 CE,AB 相交于点 D.
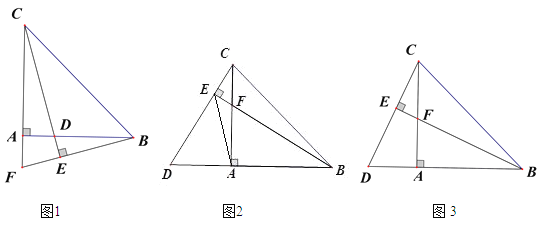
(1)如图 1,当点 F 在线段 CA 延长线上时,求证:AB+AD=CF;
(2)如图 2,当点 F 在线段 CA 上时,连接 EA,求证:EA 平分∠DEB;
(3)如图 3,当点 F 恰好为线段 CA 的中点时,EF=1,试求△BDE 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①如图1,已知![]() ,
,![]() ,可得
,可得![]() __________.
__________.

②如图2,在①的条件下,如果![]() 平分
平分![]() ,则
,则![]() __________.
__________.

③如图3,在①、②的条件下,如果![]() ,则
,则![]() __________.
__________.

(2)尝试解决下面问题:已知如图4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com