
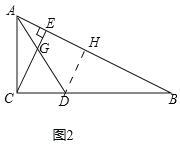
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 为
为![]() 边上一点.
边上一点.
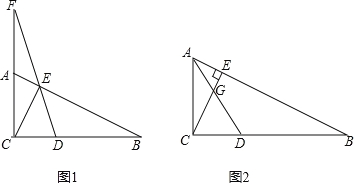
(1)当![]() 时,直接写出
时,直接写出![]() ,
,![]() .
.
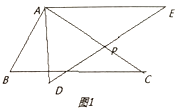
(2)如图1,当![]() ,
,![]() 时,连
时,连![]() 并延长交
并延长交![]() 延长线于
延长线于![]() ,求证:
,求证:![]() .
.
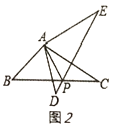
(3)如图2,连![]() 交
交![]() 于
于![]() ,当
,当![]() 且
且![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用相似三角形的判定可得![]() ,列出比例式即可求出结论;
,列出比例式即可求出结论;
(2)作![]() 交
交![]() 于
于![]() ,设
,设![]() ,则
,则![]() ,根据平行线分线段成比例定理列出比例式即可求出AH和EH,然后根据平行线分线段成比例定理列出比例式即可得出结论;
,根据平行线分线段成比例定理列出比例式即可求出AH和EH,然后根据平行线分线段成比例定理列出比例式即可得出结论;
(3)作![]() 于
于![]() ,根据相似三角形的判定可得
,根据相似三角形的判定可得![]() ,列出比例式可得
,列出比例式可得![]() ,设
,设![]() ,
,![]() ,
,![]() ,即可求出x的值,根据平行线分线段成比例定理求出
,即可求出x的值,根据平行线分线段成比例定理求出![]() ,设
,设![]() ,
,![]() ,
,![]() ,然后根据勾股定理求出AC,即可得出结论.
,然后根据勾股定理求出AC,即可得出结论.
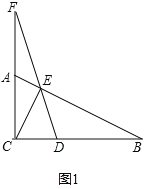
(1)如图1中,当![]() 时,
时,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() .
.
故答案为:![]() ,
,![]() .
.
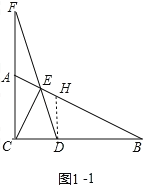
(2)如图![]() 中,作
中,作![]() 交
交![]() 于
于![]() .
.
![]() ,
,![]() ,
,
∴tan∠B=![]() ,tan∠ACE= tan∠B=
,tan∠ACE= tan∠B=![]()
∴BE=2CE,![]()
![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
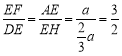 ,
,
![]() .
.
(3)如图2中,作![]() 于
于![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
则有![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】为进一步普及足球知识,传播足球文化,某市在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:

(1)获得一等奖的学生有 人;
(2)在本次知识竞赛活动中,A,B,C,D 四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是原点,矩形
是原点,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一个交点为点
轴的另一个交点为点![]() .
.
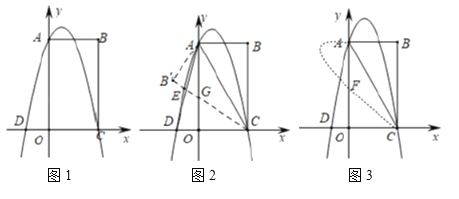
(1)如图1,求抛物线的函数表达式;
(2)如图2,连接![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠后与
折叠后与![]() 、
、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(3)如图3,将抛物线在![]() 上方的部分沿
上方的部分沿![]() 折叠后与
折叠后与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
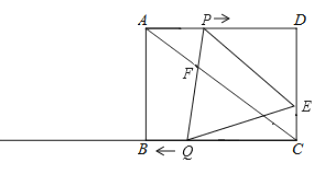
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,速度是
匀速运动,速度是![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,同时,点
,同时,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向,在射线
方向,在射线![]() 上匀速运动,速度是
上匀速运动,速度是![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与
与![]() 交与点
交与点![]() ,设运动时间为
,设运动时间为![]() .
.
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 的面积为矩形
的面积为矩形![]() 面积的
面积的![]() ;
;
(4)是否存在某一时刻![]() ,使得点
,使得点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
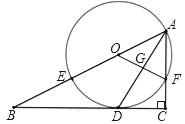
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕顶点
绕顶点![]() 逆时针旋转时,当
逆时针旋转时,当![]() 时,设
时,设![]() 与
与![]() 于
于![]() ,证明:
,证明:![]() 是等边三角形;
是等边三角形;
(2)如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕顶点
绕顶点![]() 逆时针旋转
逆时针旋转![]() 多少度时,
多少度时,![]() ,使得
,使得![]() 的顶点
的顶点![]() 落在
落在![]() 上?
上?
(3)当直角三角形变为一般三角形时,如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可以得到
,可以得到![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com