
阅读材料:多边形边上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.下图给出了四边形的具体分割方法,分别将四边形分割成了2个、3个、4个小三角形.

请你按照上述方法将下图中的五边形进行分割,并写出得到的小三角形的个数.试把这一结论推广到n边形.
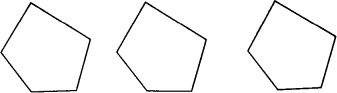
科目:初中数学 来源: 题型:阅读理解
 24、阅读下列材料,然后回答文后问题.
24、阅读下列材料,然后回答文后问题.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读材料:多边形的顶点、边上或内部的一点与多边形各顶点的连线,能够将多边形分割成若干个小三角形。如图给出了四边形的具体分割方法,分别将四边形分割成2个、3个、4个小三角形,可以得到四边形的内角和为360°。

(1)请你按照上述方法将图中的五边形进行分割,并写出得到的小三角形的个数;
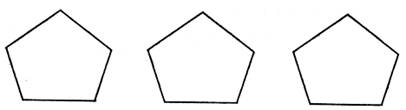
分别分割成 、 、 个小三角形;
(2)试把这一结论推广至![]() 边形,分别写出按照上述三种分割方法得到的小三角形的个数(按规律写出结论即可,可以不画图),并根据其中的一种分割方法推导出
边形,分别写出按照上述三种分割方法得到的小三角形的个数(按规律写出结论即可,可以不画图),并根据其中的一种分割方法推导出![]() 边形的内角和(画出示意图)。
边形的内角和(画出示意图)。
![]() 边形:分割成 、 、 个小三角形。试推导
边形:分割成 、 、 个小三角形。试推导![]() 边形的内角和。
边形的内角和。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com