
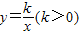 在第一象限图象上的两个点,C,D是函数
在第一象限图象上的两个点,C,D是函数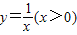 上两点,AC∥BD∥x轴,若
上两点,AC∥BD∥x轴,若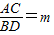 ,则△COD的面积是 (用含m的代数式表示).
,则△COD的面积是 (用含m的代数式表示).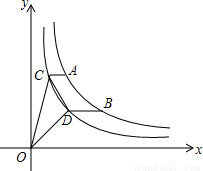
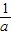 ),D(b,
),D(b,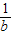 ),再由A,B是函数
),再由A,B是函数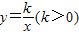 在第一象限图象上的两个点,AC∥BD∥x轴,得出A(ak,
在第一象限图象上的两个点,AC∥BD∥x轴,得出A(ak, ),B(bk,
),B(bk,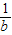 ),那么根据
),那么根据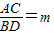 ,得出a=bm.过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,则△COD的面积=矩形ONCM的面积+梯形PDCN的面积-△COM的面积-△DOP的面积,由反比例函数系数k的几何意义,可知矩形ONCM的面积=1,△COM的面积=△DOP的面积=
,得出a=bm.过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,则△COD的面积=矩形ONCM的面积+梯形PDCN的面积-△COM的面积-△DOP的面积,由反比例函数系数k的几何意义,可知矩形ONCM的面积=1,△COM的面积=△DOP的面积= ,所以△COD的面积=梯形PDCN的面积,根据梯形的面积公式即可求解.
,所以△COD的面积=梯形PDCN的面积,根据梯形的面积公式即可求解.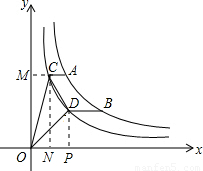 解:∵C,D是函数
解:∵C,D是函数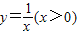 上两点,
上两点, ),D(b,
),D(b,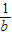 ),
),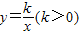 在第一象限图象上的两个点,AC∥BD∥x轴,
在第一象限图象上的两个点,AC∥BD∥x轴,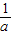 ),B(bk,
),B(bk,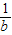 ).
).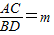 ,
,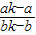 =m,
=m, (
(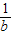 +
+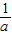 )•(b-a)-
)•(b-a)- -
-
 (
(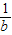 +
+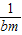 )•(b-bm)
)•(b-bm)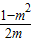 .
.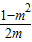 .
.

科目:初中数学 来源: 题型:
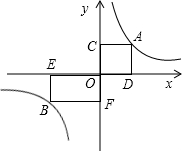 如图,A、B是函数y=
如图,A、B是函数y=| k |
| x |
| A、3 | B、6 | C、9 | D、12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•成都一模)如图,A,B是函数y=
(2013•成都一模)如图,A,B是函数y=| k |
| x |
| 1 |
| x |
| AC |
| BD |
| 1-m2 |
| 2m |
| 1-m2 |
| 2m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
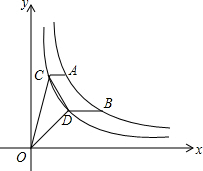 如图,A,B是函数
如图,A,B是函数 在第一象限图象上的两个点,C,D是函数
在第一象限图象上的两个点,C,D是函数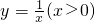 上两点,AC∥BD∥x轴,若
上两点,AC∥BD∥x轴,若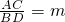 ,则△COD的面积是________(用含m的代数式表示).
,则△COD的面积是________(用含m的代数式表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com