
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为![]() 的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.
的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.

(1)画出旋转后的Rt△ADE;
(2)求出Rt△ADE的直角边DE被⊙M截得的弦PQ的长度;
(3)判断Rt△ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
|
(1)如图Rt
(2)2 (3)AD与⊙M相切 6分 证法一:过点M作MH⊥AD于H,连接MN,MA,则MN⊥AE且MN= 在Rt△AMN中,tan∠MAN= ∵∠DAE=∠BAC=60° ∴∠MAD=30° ∴∠MAN=∠MAD=30° ∴MH=MN(由△MHA≌△MNA或解Rt△AMH求得MH= ∴AD与⊙M相切 10分 证法二:连接MA、ME、MD,则S 过M作MH⊥AD于H,MG⊥DE于G,连接MN,则MN⊥AE且MN= ∴ 由此可以计算出MH= ∴AD与⊙M相切 10分 |


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
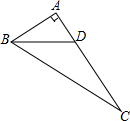 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com