
如图.等腰直角三角形ABC中,∠A=90°,P为BC的中点,小明拿着含45°角的透明三角形,使45°角的顶点落在点P,且绕P旋转.
(1)如图①:当三角板的两边分别AB、AC交于E、F点时,试说明△BPE∽△CFP.
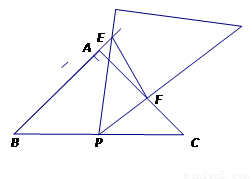
(2)将三角板绕点P旋转到图②,三角板两边分别交BA延长线和边AC于点EF.
探究1:△BPE与△CFP.还相似吗?(只需写结论)
探究2:连接EF,△BPE与△EFP是否相似?请说明理由.
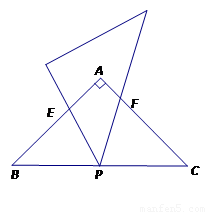
(1)证明:∵在△ABC中,∠ A=90°,AB=AC,
∴∠B=∠C=45°.
∵∠EPC=∠EPF+∠FPC=∠B+∠BEP,∠EPF=45°
∴∠BEP=∠FPC,
∵∠B=∠C
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①△BPE∽△CFP;②△BPE与△PFE相似.
下面证明结论:
同(1),可证△BPE∽△CFP,得 CP:BE=PF:PE,而CP=BP,因此 BP:BE=PF:PE.
又因为∠EBP=∠EPF,所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
【解析】(1)找出△BPE与△CFP的对应角,利用三角形一外角等于和它不相邻的两内角和性质列出等式,得出∠BPE=∠CFP,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是
如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )
如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )A、 | B、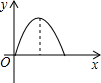 | C、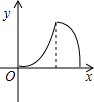 | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.
如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.| AD |
| AE |
| ||
| AC |
| DB |
| DA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com