
【题目】正方形ABCD的边长为3,如图将正方形ABCD点沿对角线BD折叠使点C与点A重合,在BD上取一点E,过E作EF⊥AD于F.继续将△EFD沿EF折叠使D与AF上点M重合,M恰好为AF的中点,设BE的中点为P,连接PF,则PF的长为__________.
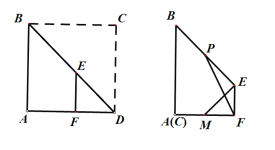
【答案】![]()
【解析】
将△EFD沿EF折叠使D与AF上点M重合,则FD=MF.M恰好为AF的中点,故AM=MF=FD=1,
由于EF⊥AD,则FE∥AB,则∠FED=∠BAD=45°,故可知△EFD为直角等腰直角三角形,则EF=FD=1,连接PM,由FE∥AB,则知四边形BAFE为梯形.在梯形BAFE中,P、M分别为BE、AF的中点,根据中位线定理可知PM![]() AF,在Rt△PMF中根据勾股定理即课求得PF的大小.
AF,在Rt△PMF中根据勾股定理即课求得PF的大小.
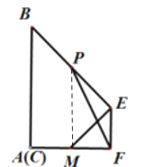
将△EFD沿EF折叠使D与AF上点M重合,
则FD=MF.
M恰好为AF的中点,正方形边长为3,
则AM=MF=FD=1.
EF⊥AD,BA⊥AD,
则FE∥AB.
∠FED=∠BDA=45°=∠FDE,
故△EFD为直角等腰直角三角形,
则EF=FD=1,
连接PM,在梯形BAFE中,P、M分别为BE、AF的中点,
根据中位线定理可知PM∥BA,故PM![]() AF,且PM=
AF,且PM=![]() =
=![]() =2.
=2.
在Rt△PMF中,PM=2,MF=1,
![]() =
=![]() +
+![]() ,
,
故PF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:
①以![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() ,
,![]() 于点
于点![]() ;
;
②画一条射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与第②步中所画的弧相交于点
长为半径画弧,与第②步中所画的弧相交于点![]() ;
;
④过点![]() 画射线
画射线![]() ,则
,则![]() .
.
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出![]() (请保留作图痕迹).
(请保留作图痕迹).
(2)完成下面证明![]() 的过程(注:括号里填写推理的依据).
的过程(注:括号里填写推理的依据).
证明:由作法可知![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ( )
( )
∴![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(探究发现)
如图1,![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 两条对角线的交点处,
两条对角线的交点处,![]() ,将
,将![]() 绕点
绕点![]() 旋转,旋转过程中,
旋转,旋转过程中,![]() 的两边分别与正方形
的两边分别与正方形![]() 的边
的边![]() 和
和![]() 交于点
交于点![]() 和点
和点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合).则
不重合).则![]() 之间满足的数量关系是 .
之间满足的数量关系是 .
(2)(类比应用)
如图2,若将(1)中的“正方形![]() ”改为“
”改为“![]() 的菱形
的菱形![]() ”,其他条件不变,当
”,其他条件不变,当![]() 时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)(拓展延伸)
如图3,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() ,且
,且![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上任取一点M(![]() )、把线段MB绕M点逆时针旋转90°至MC.连接AC,作AC的垂直平分线交AM于N点,此时AN、MN、BM为边的三角形是一个直角三角形,我们称点M,N是线段AB的勾股分割点.如下右图,已知:点M,N是线段AB的勾股分割点,
)、把线段MB绕M点逆时针旋转90°至MC.连接AC,作AC的垂直平分线交AM于N点,此时AN、MN、BM为边的三角形是一个直角三角形,我们称点M,N是线段AB的勾股分割点.如下右图,已知:点M,N是线段AB的勾股分割点,![]() ,△ABC、△MND分别是以AB、MN为斜边的等腰直角三角形,且点C与点D在AB的同侧,若MN=3,连接CD,则CD=______.
,△ABC、△MND分别是以AB、MN为斜边的等腰直角三角形,且点C与点D在AB的同侧,若MN=3,连接CD,则CD=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海监船以60海里/时的速度从A处出发沿正西方向巡逻,一可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西![]() 方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西
方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西![]() 方同.(以下结果保留根号)
方同.(以下结果保留根号)
(1)求B,C两处之问的距离;
(2)求海监船追到可疑船只所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
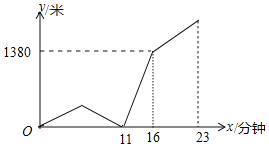
【题目】一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的![]() 快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com