
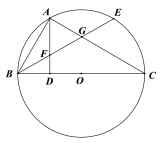
【题目】如图,BC是⊙O的直径,点A在⊙上,AD⊥BC,垂足为D,![]() ,BE分别交AD、AC与点F、G.
,BE分别交AD、AC与点F、G.
(1)证明:FA=FB.
(2)BD=DO=2,求弧EC的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据BC是⊙O的直径,AD⊥BC,![]() ,推出∠ABE=∠BAD,即可推得FA=FB.
,推出∠ABE=∠BAD,即可推得FA=FB.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据![]() ,求出∠EOC=60°,即可求出弧EC的长度是多少.
,求出∠EOC=60°,即可求出弧EC的长度是多少.
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠BAD+∠CAD=90°;
又∵AD⊥BC,
∴∠C+∠CAD=90°;
∴∠BAD=∠C,
∵![]() ,
,
∴∠C=∠ABE,
∴∠BAD=∠ABE
∴ FA=FB;
(2)连接OA、OE.
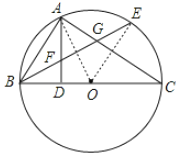
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴ AB=OA=OB=4
∴ △OAB是等边三角形,
∴∠AOB=60°,
∵![]() ,
,
∴∠AOE=60°,
∴ ∠EOC=60°
∴弧EC的长为:![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】问题探究:如图①,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .线段
.线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中线.
的中线.
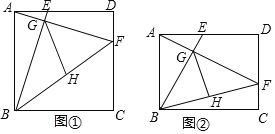
(1)求证:![]() .
.
(2)判断线段![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
问题拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() 是
是![]() 的中线,则线段
的中线,则线段![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )
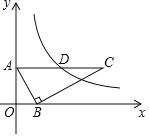
A.4B.5C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
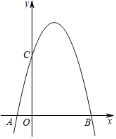
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,已知OA=1,OC=OB.
(1)求抛物线的解析式;
(2)若D(2,m)在该抛物线上,连接CD,DB,求四边形OCDB 的面积;
(3)设E是该抛物线上位于对称轴右侧的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点E作EH⊥x轴于点H,再过点F作FG⊥x轴于点G,得到矩形EFGH.在点E运动的过程中,当矩形EFGH为正方形时,求出该正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
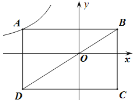
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,点A在函数![]() (
(![]() ≠0,
≠0,![]() <0)的图象上,点C的坐标为(2,
<0)的图象上,点C的坐标为(2,![]() ),则
),则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
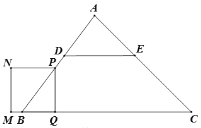
【题目】如图,在△ABC中, tan∠ABC=![]() ,∠C=45°,点D、E分别是边AB、AC上的点,且DE∥BC,BD=DE=5,动点P从点B出发,沿B-D-E-C向终点C运动,在BD-DE上以每秒5个单位长度的速度运动,在EC上以每秒
,∠C=45°,点D、E分别是边AB、AC上的点,且DE∥BC,BD=DE=5,动点P从点B出发,沿B-D-E-C向终点C运动,在BD-DE上以每秒5个单位长度的速度运动,在EC上以每秒![]() 个单位长度的速度运动,过点P作PQ⊥BC于点Q,以PQ为边作正方形PQMN,使点B、点N始终在PQ同侧. 设点P的运动时间为
个单位长度的速度运动,过点P作PQ⊥BC于点Q,以PQ为边作正方形PQMN,使点B、点N始终在PQ同侧. 设点P的运动时间为![]() (
(![]() )(
)(![]() >0),正方形PQMN与△ABC重叠部分图形的面积为S.
>0),正方形PQMN与△ABC重叠部分图形的面积为S.
(1)当点P在BD-DE上运动时,用含![]() 的代数式表示线段DP的长.
的代数式表示线段DP的长.
(2)当点N落在AB边上时,求![]() 的值.
的值.
(3)当点P在DE上运动时,求S与![]() 之间的函数关系式.
之间的函数关系式.
(4)当点P出发时,有一点H从点D出发,在线段DE上以每秒5个单位长度的速度沿D-E-D连续做往返运动,直至点P停止运动时,点H也停止运动.连结HN,直接写出HN与DE所夹锐角为45°时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为![]() 的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
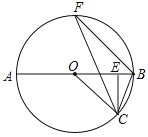
(1)求证:∠OCF=∠ECB;
(2)当AB=10,BC=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
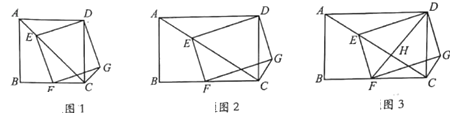
【题目】在矩形ABCD中,AB=a,AD=b,点E为对角线AC上一点,连接DE,以DE为边,作矩形DEFG,点F在边BC上;
(1)观察猜想:如图1,当a=b时,![]() =______,∠ACG=______;
=______,∠ACG=______;
(2)类比探究:如图2,当a≠b时,求![]() 的值(用含a、b的式子表示)及∠ACG的度数;
的值(用含a、b的式子表示)及∠ACG的度数;
(3)拓展应用:如图3,当a=6,b=8,且DF⊥AC,垂足为H,求CG的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com