
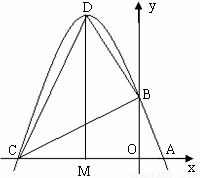
如图所示,已知m、n是方程 的两个实数根,且m<n,抛物线
的两个实数根,且m<n,抛物线 的图像经过点A(m,0)、B(0,n).
的图像经过点A(m,0)、B(0,n).
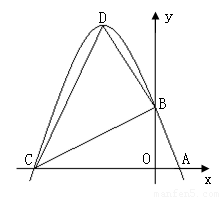
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(注:抛物线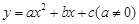 的顶点坐标为
的顶点坐标为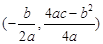
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比
为2:3的两部分,请求出P点的坐标.
(1) ;(2)C(-5,0),D(-2,9),15;(3)
;(2)C(-5,0),D(-2,9),15;(3) 或
或
【解析】
试题分析:(1)先解方程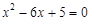 得
得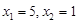 ,即可得到点A、B的坐标,再将A、B的坐标分别代入
,即可得到点A、B的坐标,再将A、B的坐标分别代入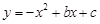 ,即可得到结果;
,即可得到结果;
(2)由 ,令y=0,即可求得C点的坐标,再由顶点坐标公式计算得点D的坐标,过D作x轴的垂线交x轴于M,则
,令y=0,即可求得C点的坐标,再由顶点坐标公式计算得点D的坐标,过D作x轴的垂线交x轴于M,则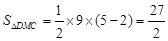 ,
,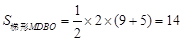 ,
,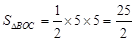 ,
,
所以 ;
;
(3)设P点的坐标为(a,0),由线段BC过B、C两点即可求得BC所在的直线方程,从而得到PH与直线BC的交点坐标,表示出PH与抛物线 的交点坐标,再分①
的交点坐标,再分① ,②
,②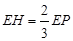 两种情况即可求得结果.
两种情况即可求得结果.
(1)解方程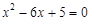 ,得
,得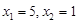
由m<n,有m=1,n=5 所以点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入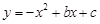 .
.
得 解这个方程组,得
解这个方程组,得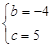
所以抛物线的解析式为 ;
;
(2)由 ,令y=0,得
,令y=0,得
解这个方程,得
所以C点的坐标为(-5,0).
由顶点坐标公式计算,得点D(-2,9).
过D作x轴的垂线交x轴于M
则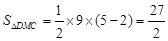
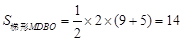 ,
,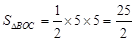
所以,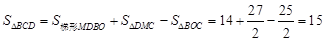 .
.
(3)设P点的坐标为(a,0)
因为线段BC过B、C两点,所以BC所在的直线方程为y=x+5.
那么,PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线 的交点坐标为
的交点坐标为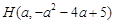
由题意得① ,即
,即
解这个方程,得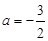 或
或 (舍去)
(舍去)
②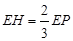 ,即
,即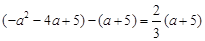
解这个方程,得 或
或 (舍去),
(舍去),
∴P点的坐标为 或
或 .
.
考点:二次函数的综合题
点评:本题知识点多,综合性强,难度较大,一般是中考压轴题,主要考查学生对二次函数的性质的熟练掌握情况.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=
如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com