
【题目】在平面直角坐标系![]() 中(如图),点
中(如图),点![]() 为直线
为直线![]() 和双曲线
和双曲线![]() 的一个交点,
的一个交点,
(1)求![]() 、
、![]() 的值;
的值;
(2)若点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,使得
,使得![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在双曲线是否存在点![]() ,使得
,使得![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在请说明理由。
的坐标;若不存在请说明理由。

【答案】(1)k=-![]() ,m=-4;(2)点P的坐标为(4,-1)或(-12,3);(3)M(
,m=-4;(2)点P的坐标为(4,-1)或(-12,3);(3)M(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法即可解决问题.
(2)如图1中,设直线y=-![]() x与反比例函数y=-
x与反比例函数y=-![]() 的另一个交点为C(4,-1).由对称性可知:OA=OC,推出当点P与C重合时,S△ABP=2S△ABO,此时P(4,-1).当点P在OA的延长线上时,P′A=AC时,S△ABP=2S△ABO,再利用中点坐标公式求解即可.
的另一个交点为C(4,-1).由对称性可知:OA=OC,推出当点P与C重合时,S△ABP=2S△ABO,此时P(4,-1).当点P在OA的延长线上时,P′A=AC时,S△ABP=2S△ABO,再利用中点坐标公式求解即可.
(3)如图2中,将OA绕点O顺时针旋转90°得到OA′,则A′(1.4),取AA′的中点D,作直线OD在第二象限交反比例函数于M.此时∠AOM=45°,求出直线OD的解析式,再构建方程组确定点M的坐标.
(1)∵点A(-4,1)在直线y=kx和双曲线y=![]() 的图象上,
的图象上,
∴k=-![]() ,m=-4.
,m=-4.
(2)如图1中,设直线y=-![]() x与反比例函数y=-
x与反比例函数y=-![]() 的另一个交点为C(4,-1).
的另一个交点为C(4,-1).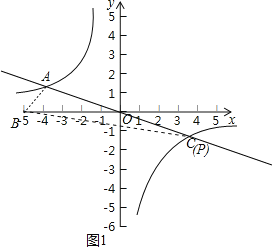
由对称性可知:OA=OC,
∴当点P与C重合时,S△ABP=2S△ABO,此时P(4,-1).
当点P在OA的延长线上时,P′A=AC时,S△ABP=2S△ABO,此时P′(-12,3),
综上所述,满足条件的点P的坐标为(4,-1)或(-12,3).
(3)如图2中,将OA绕点O顺时针旋转90°得到OA′,则A′(1.4),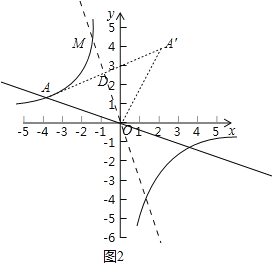
取AA′的中点D,作直线OD在第二象限交反比例函数于M.此时∠AOM=45°,
∵D(-![]() ),
),
∴直线OD的解析式为y=-![]() x,
x,
由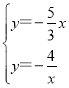 ,解得
,解得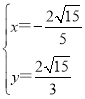 或
或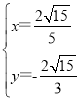 ,
,
∵点M在第二象限,
∴M(![]() ,
,![]() ).
).


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】一玩具城以![]() 元/个的价格购进某种玩具进行销售,并预计当售价为
元/个的价格购进某种玩具进行销售,并预计当售价为![]() 元/个时,每天能售出
元/个时,每天能售出![]() 个玩具,且在一定范围内,当每个玩具的售价平均每提高
个玩具,且在一定范围内,当每个玩具的售价平均每提高![]() 元时,每天就会少售出
元时,每天就会少售出![]() 个玩具
个玩具
![]() 若玩具售价不超过
若玩具售价不超过![]() 元/个,每天售出玩具总成本不高于
元/个,每天售出玩具总成本不高于![]() 元,预计每个玩具售价的取值范围;
元,预计每个玩具售价的取值范围;
![]() 在实际销售中,玩具城以
在实际销售中,玩具城以![]() 中每个玩具的最低售价及相应的销量为基础,进一步调整了销售方案,将每个玩具的售价提高了
中每个玩具的最低售价及相应的销量为基础,进一步调整了销售方案,将每个玩具的售价提高了![]() ,从而每天的销售量降低了
,从而每天的销售量降低了![]() ,当每天的销售利润为
,当每天的销售利润为![]() 元时,求
元时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京、上海相距约300 km,快车与慢车的速度分别为100 km/ h和50 km/ h,两车同时从南京出发,匀速行驶,快车到达上海后,原路返回南京,慢车到达上海后停止.设两车出发后的时间为x h,快车、慢车行驶过程中离南京的路程为y1、y2 km.
(1)求y1、y2与x之间的函数关系式,并在下列平面直角坐标系中画出它们的图像;
(2)若镇江、南京相距约80 km,求两车经过镇江的时间间隔;
(3)直接写出出发多长时间,两车相距100 km.

查看答案和解析>>
科目:初中数学 来源: 题型:
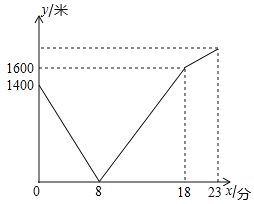
【题目】小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回![]() 两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
![]() 妈妈从家出发______分钟后与小婷相遇;
妈妈从家出发______分钟后与小婷相遇;
![]() 相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米
相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,台风中心位于点![]() ,并沿东北方向
,并沿东北方向![]() 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,![]() 市位于点
市位于点![]() 的北偏东75°方向上,距离
的北偏东75°方向上,距离![]() 点480千米.
点480千米.

(1)说明本次台风是否会影响![]() 市;
市;
(2)若这次台风会影响![]() 市,求
市,求![]() 市受台风影响的时间.
市受台风影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数![]() 的图象,小强从图象中得出了
的图象,小强从图象中得出了![]() 条信息:
条信息:
①![]() ;②
;②![]() ;③当
;③当![]() 时,函数取得最小值;④
时,函数取得最小值;④![]() ,
,
其中正确的个数有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为130平方米的仓库,现有能围成32米长的木板,仓库的一边靠墙,并在与墙垂直的一边开一道1米宽的小门.
(1)如果墙长16米,求仓库的长和宽;
(2)如果墙长a米,在离开墙9米开外仓库一侧修条小路,那么墙长至少要多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边中点,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F
(1)当点E在AC边上时(如图1),求证CE=BF
(2)在(1)的条件下,求证:![]()
(3)当∠EDF绕D点旋转到图3的位置即点E、F分别在AC、CB边的延长线上时,上述(2)结论是否成立?若成立,请给予证明;若不成立,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com