
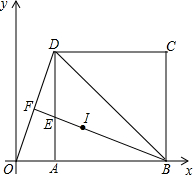
 (2013•乌鲁木齐)如图.在平面直角坐标系中,边长为
(2013•乌鲁木齐)如图.在平面直角坐标系中,边长为| 2 |

| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
|
|
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
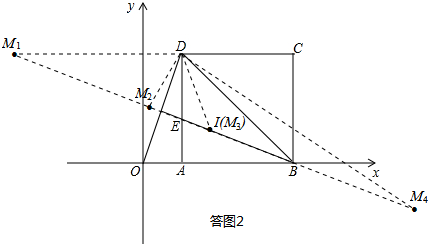
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
 (2013•乌鲁木齐)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
(2013•乌鲁木齐)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com