Question

某服装厂现有A种布料70m，B种布料52m，现计划用这两种布料生产M、N两种型号的时装80套。已知做一套M型号的时装需要A种布料0.6m，B种布料0.9m,可获利45元；做一套N型号的时装需要A种布料1.1m，B种布料0.4 m，可获利50元。若设生产N型号的时装套数为x，用这批布料生产这两种型号的时装所获的总利润为y元。
（1）求y与x的函数关系式，并求出x的取值范围；（2）该服装厂在生产这批时装中，当生产N型号的时装多少套时，所获利润最大？最大利润是多少？

Answer 1

(1)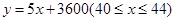;(2)当生产N型号的时装44套时,所获利润最大,最大利润是3820元．

解析考点：一次函数的应用。
分析：
（1）因为生产M、N两种型号的时装共80套，如果生产N型号的时装x套，那么生产M型号的时装为80-x，由于生产M可以获利45元，生产N型号可以获利50元，则可以到x与总利润y的关系；
（2）当布料得到最大利用，且恰当时，利润最大，A种布料不可能用的比70m多，M型号的时装需用A种布料0.6m，所以可以知道，N型号的时装需用A种布料1.1m，1.1x+0.6（80-x）≤70．
解答：
（1）由题意可知：N型号的时装x套，那么生产M型号的时装为80-x，M可以获利45元，生产N型号可以获利50元
∴y=45（80-x）+50x
即y=5x+3600；
∵A种布料不可能用的比70m多，从题意知
0.6（80-x）+1.1x≤70
∴x≤44。
又∵B种布料不可能用的比52m多，从题意知
0.9（80-x）+0.4x≤52
∴x≥40。
∴40≤x≤44；
（2）∵总利润：y=5x+3600，40≤x≤44，
∴当x=44时y=3820最大。
即N型号的时装为44套时，所获总利润最大，最大总利润是3820元。
点评：本题考查的是用一次函数解决实际问题，此类题是近年中考中的热点问题．注意利用一次函数求最值时，关键是应用一次函数的性质；即由函数y随x的变化，结合自变量的取值范围确定最值。