
【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).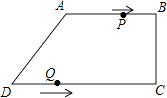
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
【答案】
(1)解:如图1:过点A作AM⊥CD于点M,
∵∠BCD=90°,
即BC⊥CD,
∴AM∥BC,
又∵AB∥CD,
∴四边形ABCM为平行四边形,
∵∠BCD=90°,
∴平行四边形ABCM为矩形,
∵AB=AD=10cm,BC=8cm,
∴AM=BC=8cm,CM=AB=10cm,
在Rt△ADM中,
∴DM=![]() =6cm,
=6cm,
∴CD=CM+MD=10+6=16cm.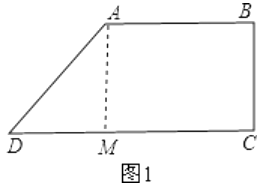
(2)解:如图2:
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,
∴PB=AB-AP=10-3t,
又∵四边形PBQD为平行四边形,
∴PB=DQ,
∴10-3t=2t,
∴t=2,
∴PB=DQ=4cm,
由(1)知CD=16cm,
∴CQ=12cm,
又∵BC=8cm,∠BCD=90°,
在Rt△BCQ中,
∴BQ=![]() =4
=4![]() cm,
cm,
∴CPBQD=2(PB+BQ)=2×(4+4![]() )=8+8
)=8+8![]() (cm).
(cm).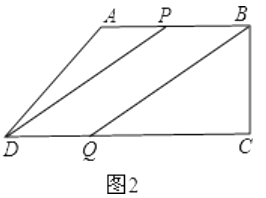
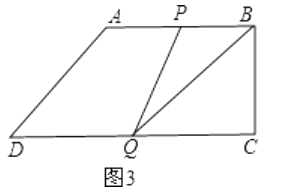
(3)解:①当P在AB上时,如图3,
∵运动时间为t,
∴AP=3t,DQ=2t,
∴0![]() 3t
3t![]() 10,
10,
∴0![]() t
t![]()
![]() ,
,
又∵AB=10cm,BC=8cm,
∴PB=AB-AP=10-3t,
∴S△BPQ=![]() .BP.BC=
.BP.BC=![]() ×(10-3t)×8=20,
×(10-3t)×8=20,
∴t=![]() .
.
②当P在BC上时,如图4,
∵运动时间为t,
∴AP=3t,DQ=2t,
∴10![]() 3t
3t![]() 18,
18,
∴![]()
![]() t
t![]() 6,
6,
又∵AB=10cm,BC=8cm,
∴PB=AB-AP=3t-10,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴S△BPQ=![]() .BP.CQ=
.BP.CQ=![]() ×(3t-10)×(16-2t)=20,
×(3t-10)×(16-2t)=20,
∴3t2-34t+100=0,
∴△=342-4×3×100=-44![]() 0,
0,
∴从方程无解.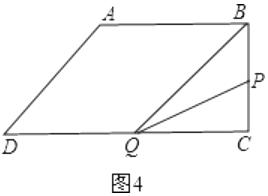
③当P在CD上时,若点P在点Q的右侧,如图5,
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,BC=8cm,
∴CP=AP-AB-BC=3t-18,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴PQ=CQ-CP=(16-2t)-(3t-18)=34-5t,
∴![]() ,
,
∴6![]() t
t![]()
![]() .
.
∴S△BPQ=![]() .PQ.BC=
.PQ.BC=![]() ×(34-5t)×8=20,
×(34-5t)×8=20,
∴t=![]()
![]() 6(不合题意,舍去).
6(不合题意,舍去).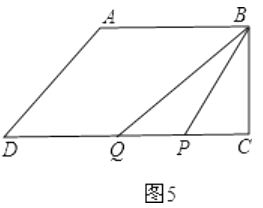
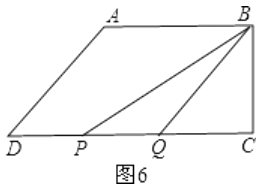
④当P在CD上时,若点P在点Q的左侧,如图6,
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,BC=8cm,
∴CP=AP-AB-BC=3t-18,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴PQ=CP-CQ=(3t-18)-(16-2t)=5t-34,
∴![]() ,
,
∴![]()
![]() t
t![]() 8.
8.
∴S△BPQ=![]() .PQ.BC=
.PQ.BC=![]() ×(5t-34)×8=20,
×(5t-34)×8=20,
∴t=![]() .
.
综上所述:当t=![]() 秒或
秒或![]() 秒时,△BPQ的面积为20cm2.
秒时,△BPQ的面积为20cm2.
【解析】(1)如图1:过点A作AM⊥CD于点M,由∠BCD=90°,AB∥CD得出四边形ABCM为矩形,在Rt△ADM中,根据勾股定理求出DM=6cm,
从而求出CD=CM+MD=10+6=16cm.
(2)如图2:由题意得出AP=3t,DQ=2t,PB=AB-AP=10-3t,由平行四边形的性质求出t的值,从而得出PB=DQ=4cm,再由勾股定理求出
BQ的值,从而求出四边形PBQD的周长.
(3)根据题意分四种情况讨论:①当P在AB上时,如图3;②当P在BC上时,如图4;③当P在CD上时,若点P在点Q的右侧,如图5;④当P在CD上时,若点P在点Q的左侧,如图6;根据题意画出符合所有条件的图形,再由三角形的面积列出方程,求出符合范围的数值即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( ) 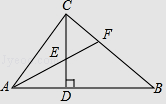
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE= ![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE. 
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中不能用平方差公式计算的是( )
A. (x-y)(-x+y)B. (-x+y)(-x-y)C. (-x-y)(x-y)D. (x+y)(-x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】支付宝与“滴滴打车”联合推出优惠,“滴滴打车”一夜之间红遍大江南北,据统计,2016年“滴滴打车”账户流水总金额达到4730000000元,用科学记数法表示为( )
A.4.73×108
B.4.73×109
C.4.73×1010
D.4.73×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com