Question

【题目】已知：两个等腰直角三角形（）边长分别为a和b（）如图放置在一起，连接AD，

（1）求阴影部分()的面积

（2）如果有一个点正好位于线段的中点，连接.得到,求的面积

（3）（2）中的三角形比（1）中的面积大还是小，大（小）多少？

Answer 1

【答案】（1）ab；（2）(a+b)2；（3）S△ADP大，大(a-b)2.

【解析】

（1）先根据梯形的定义证明四边形ACED是梯形，再利用S阴影=S梯形-S△ACB-S△DEB即可求面积；

（2）利用S△ADP=S梯形-S△ACP-S△DEP可求面积；

（3）由于a<b，易求(a-b)2>0，即可得(a2+b2)-ab>0，从而易求S△ADP>S△ABD．

解：（1）如图所示，

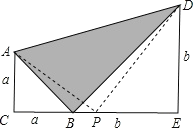
∵△ACB和△BED是等腰直角三角形，

∴∠C=∠E=90°，

∴∠C+∠E=180°，

∴AC∥DE，

∵a<b，

∴四边形ACED是梯形，

∴S阴影=S梯形-S△ACB-S△DEB

=(a+b)(a+b)-a2-b2

=ab；

（2）同（1）一样，

S△ADP=S梯形-S△ACP-S△DEP

=(a+b)(a+b)-×(a+b)a-×(a+b)b

=(a+b)2；

（3）S△ADP-S△ABD

=(a+b)2-ab

=(a-b)2

∵a<b，

∴(a-b)2>0，

∴S△ADP>S△ABD．

故答案为：（1）ab；（2）(a+b)2；（3）S△ADP大，大(a-b)2.