
【题目】对一个矩形ABCD及![]() 给出如下定义:在同一平面内,如果
给出如下定义:在同一平面内,如果![]() 上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是
上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是![]() 的“随从矩形”
的“随从矩形”![]() 如图,在平面直角坐标系xOy中,直线l:
如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,
交x轴于点M,![]() 的半径为4,矩形ABCD沿直线运动
的半径为4,矩形ABCD沿直线运动![]() 在直线l上
在直线l上![]() ,
,![]() ,
,![]() 轴,当矩形ABCD是
轴,当矩形ABCD是![]() 的“随从矩形”时,点A的坐标为______.
的“随从矩形”时,点A的坐标为______.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是一个长方形,将AD沿某一直线AF(F为折痕与CD边的交点)折叠,使点D落在BC边上的某一点E处,请用没有刻度的直尺与圆规找出点E与折痕AF,并在折痕AF上找一点P满足BP+EP最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合探究
问题情境:
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
问题初探:
如图1,在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一个动点(D与A,B不重合),连接CD,以CD为直角边作等腰直角三角形CDE,连接BE.

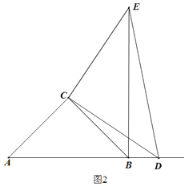

(1)当点D在线段AB上时,AD与BE的数量关系是 ;位置关系是 ;AB,BD,BE三条线段之间的关系是 .
类比再探:
(2)如图2,当点D运动到AB的延长线上时,AD与BE还存在(1)中的位置关系吗?若存在,请说明理由.同时探索AB,BD,BE三条线段之间的数量关系,并说明理由.
能力提升:
(3)如图3,当点D运动到BA的延长线上时,若AB=7,AD=2,则AE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题发现
问题发现
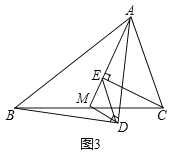
在等腰三角形ABC中,![]() ,分别以AB和AC为斜边,向
,分别以AB和AC为斜边,向![]() 的外侧作等腰直角三角形,如图1所示,其中
的外侧作等腰直角三角形,如图1所示,其中![]() 于点F,
于点F,![]() 于点G,M是BC的中点,连接MD和ME.
于点G,M是BC的中点,连接MD和ME.
填空:线段AF,AG,AB之间的数量关系是______;
线段MD,ME之间的数量关系是______.
![]() 拓展探究
拓展探究
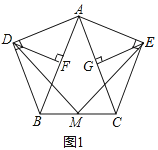
在任意三角形ABC中,分别以AB和AC为斜边向![]() 的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
![]() 解决问题
解决问题
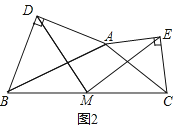
在任意三角形ABC中,分别以AB和AC为斜边,向![]() 的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若
的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若![]() ,请直接写出线段DE的长.
,请直接写出线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中
中![]() ,
,![]() ,
,![]() .
.

(1)作出![]() 关于直线
关于直线![]() 对称的图形△
对称的图形△![]() 并写出△
并写出△![]() 各顶点的坐标;
各顶点的坐标;
(2)将△![]() 向左平移2个单位,作出平移后的△
向左平移2个单位,作出平移后的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和△
和△![]() ,它们是否关于某直线对称?若是,请指出对称轴,并求
,它们是否关于某直线对称?若是,请指出对称轴,并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A.25°B.30°
C.60°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表中的每一组值:
名称组别 |
|
|
| 名称组别 |
|
|
|
第1组 | 3 |
|
| 第5组 | |||
第2组 | 5 |
|
|
|
|
| |
第3组 | 7 |
|
|
|
|
| |
第4组 | 8 |
|
| 第 |
(1)根据表中前四组![]() 、
、![]() 、
、![]() 值的变化规律,第5组中
值的变化规律,第5组中![]() ;
;![]() ;第
;第![]() 组中
组中![]() ;
;![]() ;
;![]() .
.
(2)试证明以表中每组![]() 、
、![]() 、
、![]() 为边的三角形都是直角三角形.
为边的三角形都是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
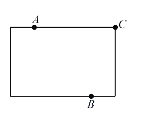
(1)为进一步打造“宜居北京”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉 ![]() 到广场的两个入口
到广场的两个入口 ![]() ,
,![]() 的距离相等,且到广场管理处
的距离相等,且到广场管理处 ![]() 的距离等于
的距离等于 ![]() 和
和 ![]() 之间距离的一半,
之间距离的一半,![]() ,
,![]() ,
,![]() 的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉
的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉 ![]() 的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
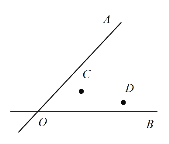
(2)如图,两条公路 ![]() 和
和 ![]() 相交于
相交于 ![]() 点,在
点,在 ![]() 的内部有工厂
的内部有工厂 ![]() 和
和 ![]() ,现要修建一个货站
,现要修建一个货站 ![]() ,使货站
,使货站 ![]() 到两条公路
到两条公路 ![]() ,
,![]() 的距离相等,且到两工厂
的距离相等,且到两工厂 ![]() ,
,![]() 的距离相等,用尺规作出货站
的距离相等,用尺规作出货站 ![]() 的位置.(要求:不写作法,保留作图痕迹,必须用铅笔作图)
的位置.(要求:不写作法,保留作图痕迹,必须用铅笔作图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com