
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 下两幅不完整的统计图表.请你根据图表提供的信息回答下列问题:
下两幅不完整的统计图表.请你根据图表提供的信息回答下列问题:| 血型 | 人数 |
| A | a |
| B | 13 |
| AB | 5 |
| O | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 的速度上升,再通过几小时,洪水将会淹到拱桥顶?
的速度上升,再通过几小时,洪水将会淹到拱桥顶?查看答案和解析>>
科目:初中数学 来源: 题型:
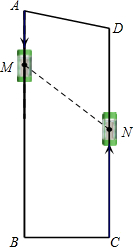 (2011•安宁市一模)随着科学技术的不断发展,人们的出行购物将会变得便捷、轻松,下图是我市未来购物商场的两部电梯的抽象图.已知:AB⊥BC于B,DC⊥BC于C,AB=26米,DC=24米,BC=8米.电梯M从A出发以1米/秒的速度匀速向下移动,同时,电梯N从C出发以2米/秒的速度匀速向上移动.因电梯还处在测试阶段,测试人员为了很好地测试电梯,规定当一个电梯到达另一个端点时,两部电梯停止移动.设电梯移动时间为t秒,请你帮测试人员先算一算:
(2011•安宁市一模)随着科学技术的不断发展,人们的出行购物将会变得便捷、轻松,下图是我市未来购物商场的两部电梯的抽象图.已知:AB⊥BC于B,DC⊥BC于C,AB=26米,DC=24米,BC=8米.电梯M从A出发以1米/秒的速度匀速向下移动,同时,电梯N从C出发以2米/秒的速度匀速向上移动.因电梯还处在测试阶段,测试人员为了很好地测试电梯,规定当一个电梯到达另一个端点时,两部电梯停止移动.设电梯移动时间为t秒,请你帮测试人员先算一算:| 26 |
| 3 |
| 26 |
| 3 |
| 28 |
| 3 |
| 28 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
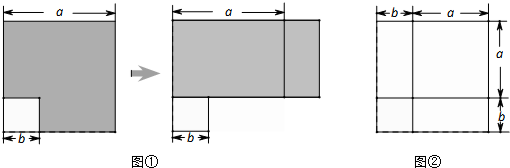
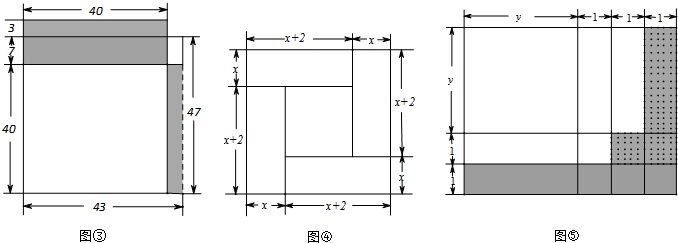
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com