
分析 (1)根据有理数的加法运算,可得答案;
(2)根据有理数的减法运算,可得答案;
(3)根据装卸都付费,可得总费用.
解答 解:(1)∵+30-25-30+28-29-16-15=-57;
∴经过这7天,仓库里的水泥减少了57吨;
(2)∵200+57=257,
∴那么7天前,仓库里存有水泥257吨.
(3)依题意:
进库的装卸费为:[(+30)+(+28)]a=58a;
出库的装卸费为:[|-25|+|-30|+|-29|+|-16|+|-15|]b=115b,
∴这7天要付多少元装卸费58a+115b.
点评 本题考查了正数和负数及列代数式的知识,(1)有理数的加法是解题关键;(2)剩下的减去多运出的就是原来的,(3)装卸都付费.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
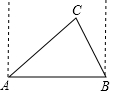 某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.
如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com