
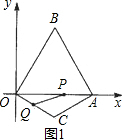
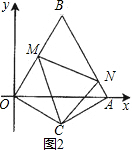
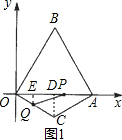
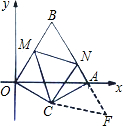
 解:(1)过点C作CD⊥OA于点D.(如图)
解:(1)过点C作CD⊥OA于点D.(如图) =
=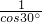 =
=
 时,OQ=t,AP=3t,OP=OA-AP=2-3t.
时,OQ=t,AP=3t,OP=OA-AP=2-3t.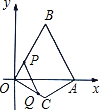
 OQ=
OQ= ,
, OP•EQ=
OP•EQ= (2-3t)•
(2-3t)• =-
=-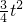 +
+ t,
t,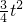 +
+ t;
t; <t≤
<t≤ 时(如图)
时(如图) OQ•OP=
OQ•OP= t•(3t-2)=
t•(3t-2)=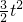 -t,
-t,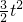 -t;
-t; 时,S=-
时,S=-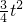 +
+ t,当
t,当 <t≤
<t≤ 时,S=
时,S=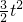 -t
-t ,1)或(
,1)或( ,0)或(
,0)或( ,0)或(
,0)或( ,
, )
)
 ,
, 秒,点P从点A→O→B需要
秒,点P从点A→O→B需要 秒,所以分两种情况讨论:①0<t<
秒,所以分两种情况讨论:①0<t< ;②
;② ≤t<
≤t< .针对每一种情况,根据P点所在的位置,由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系,并且得出自变量t的取值范围;
.针对每一种情况,根据P点所在的位置,由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系,并且得出自变量t的取值范围;

 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
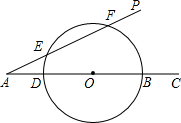 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:
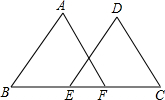 已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD
已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com